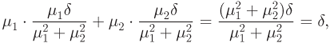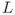Copyright 2017 by John Wiley & Sons, Inc. All rights reserved.
Published by John Wiley & Sons, Inc., Hoboken, New Jersey.
Published simultaneously in Canada.
No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 646-8600, or on the web at www.copyright.com. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008.
Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representations or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives or written sales materials. The advice and strategies contained herein may not be suitable for your situation. You should consult with a professional where appropriate. Neither the publisher nor author shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages.
For general information on our other products and services please contact our Customer Care Department with the U.S. at 877-762-2974, outside the U.S. at 317-572-3993 or fax 317-572-4002.
Wiley also publishes its books in a variety of electronic formats. Some content that appears in print, however, may not be available in electronic format.
Library of Congress Cataloging-in-Publication Data:
Leonard, I. Ed., 1938
Geometry of convex sets / I.E. Leonard, J.E. Lewis.
pages cm
Includes bibliographical references and index.
ISBN 978-1-119-02266-4 (cloth) | ISBN 978-1-119-18418-8 (solutions manual)
1. Convex sets. 2. Geometry. I. Lewis, J. E. (James Edward) II. Title.
QA640.L46 2016
516.08dc23
2015021566
Preface
These are the solutions to the odd numbered problems in the text The Geometry of Convex Sets by I. E. Leonard and J. E. Lewis.
Some of the solutions are from assignments we gave in class, some are not. In all of the solutions, we have provided details that added to the clarity and ease of understanding for beginning students, and when possible to the elegance of the solutions.
Ed and Ted
Edmonton, Alberta, Canada
March 2016
Chapter 1
Introduction to N-Dimensional Geometry
1.2 Points, Vectors, and Parallel Lines
1.2.5 Problems
A remark about the exercises is necessary. Certain questions are phrased as statements to avoid the incessant use of prove that. See Problem 1, for example. Such statements are supposed to be proved. Other questions have a truefalse or yesno quality. The point of such questions is not to guess, but to justify your answer. Questions marked with  are considered to be more challenging. Hints are given for some problems. Of course, a hint may contain statements that must be proved.
are considered to be more challenging. Hints are given for some problems. Of course, a hint may contain statements that must be proved.
- Let
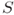 be a nonempty set in
be a nonempty set in 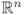 . If every three points of
. If every three points of 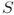 are collinear, then
are collinear, then 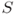 is collinear.
is collinear.
Solution
Let 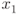 and
and 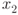 be two distinct points in
be two distinct points in 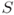 , then there is a unique line
, then there is a unique line 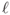 passing through these two points. Now let
passing through these two points. Now let 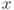 be an arbitrary point in
be an arbitrary point in 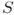 , from the hypothesis,
, from the hypothesis, 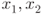 , and
, and 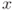 must be on some line
must be on some line 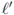 , and since
, and since 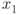 and
and 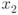 uniquely determine the line
uniquely determine the line 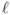 , we must have
, we must have 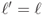 . Therefore, every point
. Therefore, every point 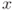 in
in 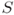 is on the line
is on the line 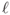 .
.
- Given that the line
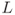 has the linear equation
has the linear equation show that the point
is on the line, and that the vector 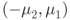 is parallel to the line.
is parallel to the line.
Hint. If 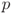 is on the line and if
is on the line and if 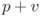 is also on the line, then
is also on the line, then 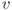 must be parallel to the line.
must be parallel to the line.
Solution
Substituting the coordinates of this point into the linear equation for 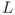 , we see that
, we see that
so that the given point is on 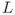
Next page














 are considered to be more challenging. Hints are given for some problems. Of course, a hint may contain statements that must be proved.
are considered to be more challenging. Hints are given for some problems. Of course, a hint may contain statements that must be proved.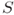 be a nonempty set in
be a nonempty set in 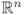 . If every three points of
. If every three points of 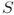 are collinear, then
are collinear, then 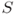 is collinear.
is collinear. 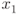 and
and 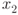 be two distinct points in
be two distinct points in  , then there is a unique line
, then there is a unique line 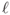 passing through these two points. Now let
passing through these two points. Now let 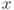 be an arbitrary point in
be an arbitrary point in 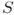 , from the hypothesis,
, from the hypothesis, 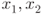 , and
, and 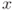 must be on some line
must be on some line 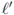 , and since
, and since 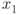 and
and 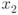 uniquely determine the line
uniquely determine the line 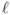 , we must have
, we must have 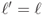 . Therefore, every point
. Therefore, every point 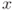 in
in 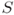 is on the line
is on the line 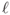 .
.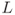 has the linear equation
has the linear equation 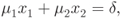
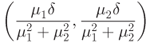
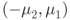 is parallel to the line.
is parallel to the line.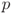 is on the line and if
is on the line and if 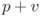 is also on the line, then
is also on the line, then 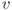 must be parallel to the line.
must be parallel to the line.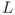 , we see that
, we see that