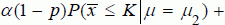Copyright 2013 by John Wiley & Sons, Inc.
Published by John Wiley & Sons, Inc., Hoboken, New Jersey. All rights reserved. Published simultaneously in Canada.
No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 750-4470, or on the web at www.copyright.com . Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street,
Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at
http://www.wiley.com/go/permission .
Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representation or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives or written sales materials. The advice and strategies contained herein may not be suitable for your situation. You should consult with a professional where appropriate. Neither the publisher nor author shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages.
For general information on our other products and services please contact our Customer Care
Department within the United States at (800) 762-2974, outside the United States at (317) 572-3993 or fax (317) 572-4002.
Wiley also publishes its books in a variety of electronic formats. Some content that appears in print, however, may not be available in electronic formats. For more information about Wiley products, visit our web site at www.wiley.com.
Library of Congress Cataloging-in-Publication Data is available.
ISBN 978-1-118-76237-0
CHAPTER 1:
INTRODUCTION
1.1 In the figure below, xmin and xmax denote optimal solutions for Part (a) and Part (b), respectively.
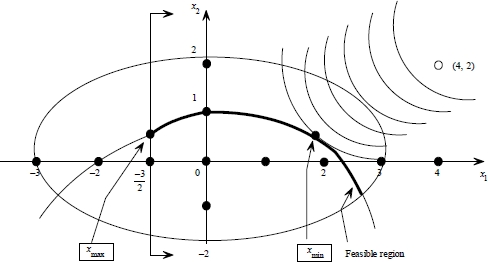
1.2 a. The total cost per time unit (day) is to be minimized given the storage limitations, which yields the following model:
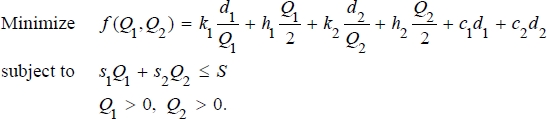
Note that the last two terms in the objective function are constant and thus can be ignored while solving this problem.
b. Let
Sj denote the lost sales (in each cycle) of product
j,
j = 1, 2. In this case, we replace the objective function in Part (a) with
F(
Q1,
Q2,
S1,
S2), where
F(
Q1,
Q2,
S1,
S2) =
F1(
Q1,
S1) +
F2(
Q2,
S2), and where
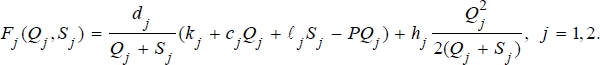
This follows since the cycle time is
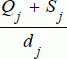
, and so over some
T days, the number of cycles is
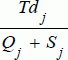
. Moreover, for each cycle, the fixed setup cost is
kj, the variable production cost is
cjQj, the lost sales cost is
ljSj, the profit (negative cost) is
PQj, and the inventory carrying cost is
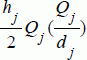
. This yields the above total cost function on a daily basis.
1.4| Notation: | xj : production in period j, j = 1,,n |
| dj : demand in period j, j = 1,,n |
| Ij : inventory at the end of period j, j = 0, 1,,n. |
The production scheduling problem is to:
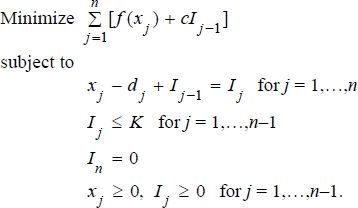
1.6 Let
X denote the set of feasible portfolios. The task is to find an
x*
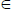 X
X such that there does not exist an
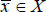
for which
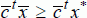
and
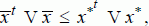
with at least one inequality strict. One way to find is to solve:
Maximize
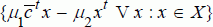
for different values of (1, 2) > 0 such that 1 + 2 = 1.
1.10 Let x and p denote the demand and production levels, respectively, and let Z denote a standard normal random variable. Then we need p to be such that P(p < x 5) 0.01, which by the continuity of the normal random variable is equivalent to P(xp + 5) 0.01. Therefore, p must satisfy
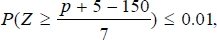
where
Z is a standard normal random variable. From tables of the standard normal distribution we have
P(
Z 2.3267) = 0.01. Thus, we want
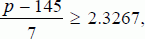
or that the chance constraint is equivalent to
p 161.2869.
1.13 We need to find a positive number
K that minimizes the expected total cost. The expected total cost is
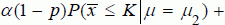









![Hanif Kureishi [Hanif Kureishi] - What Happened?](/uploads/posts/book/141306/thumbs/hanif-kureishi-hanif-kureishi-what-happened.jpg)







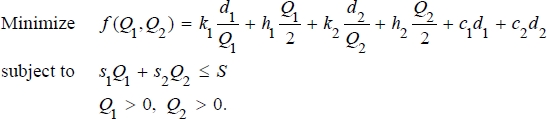
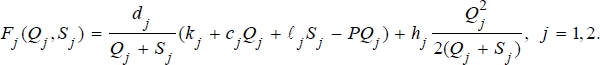
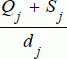 , and so over some T days, the number of cycles is
, and so over some T days, the number of cycles is 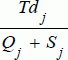 . Moreover, for each cycle, the fixed setup cost is kj, the variable production cost is cjQj, the lost sales cost is ljSj, the profit (negative cost) is PQj, and the inventory carrying cost is
. Moreover, for each cycle, the fixed setup cost is kj, the variable production cost is cjQj, the lost sales cost is ljSj, the profit (negative cost) is PQj, and the inventory carrying cost is 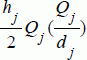 . This yields the above total cost function on a daily basis.
. This yields the above total cost function on a daily basis.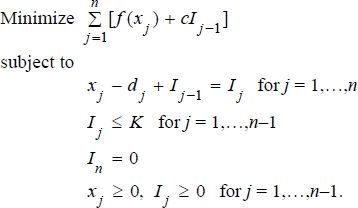
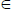 X such that there does not exist an
X such that there does not exist an 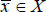 for which
for which 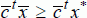 and
and 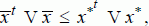 with at least one inequality strict. One way to find is to solve:
with at least one inequality strict. One way to find is to solve: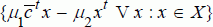
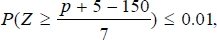
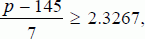 or that the chance constraint is equivalent to p 161.2869.
or that the chance constraint is equivalent to p 161.2869.