1.1 Optimization
The concept of optimization is now well rooted as a principle underlying the analysis of many complex decision or allocation problems. It offers a certain degree of philosophical elegance that is hard to dispute, and it often offers an indispensable degree of operational simplicity. Using this optimization philosophy, one approaches a complex decision problem, involving the selection of values for a number of interrelated variables, by focusing attention on a single objective designed to quantify performance and measure the quality of the decision. This one objective is maximized (or minimized, depending on the formulation) subject to the constraints that may limit the selection of decision variable values. If a suitable single aspect of a problem can be isolated and characterized by an objective, be it profit or loss in a business setting, speed or distance in a physical problem, expected return in the environment of risky investments, or social welfare in the context of government planning, optimization may provide a suitable framework for analysis.
It is, of course, a rare situation in which it is possible to fully represent all the complexities of variable interactions, constraints, and appropriate objectives when faced with a complex decision problem. Thus, as with all quantitative techniques of analysis, a particular optimization formulation should be regarded only as an approximation. Skill in modeling, to capture the essential elements of a problem, and good judgment in the interpretation of results are required to obtain meaningful conclusions. Optimization, then, should be regarded as a tool of conceptualization and analysis rather than as a principle yielding the philosophically correct solution.
Skill and good judgment, with respect to problem formulation and interpretation of results, is enhanced through concrete practical experience and a thorough understanding of relevant theory. Problem formulation itself always involves a tradeoff between the conflicting objectives of building a mathematical model sufficiently complex to accurately capture the problem description and building a model that is tractable. The expert model builder is facile with both aspects of this tradeoff. One aspiring to become such an expert must learn to identify and capture the important issues of a problem mainly through example and experience; one must learn to distinguish tractable models from nontractable ones through a study of available technique and theory and by nurturing the capability to extend existing theory to new situations.
This book is centered around a certain optimization structurethat characteristic of linear and nonlinear programming. Examples of situations leading to this structure are sprinkled throughout the book, and these examples should help to indicate how practical problems can be often fruitfully structured in this form. The book mainly, however, is concerned with the development, analysis, and comparison of algorithms for solving general subclasses of optimization problems. This is valuable not only for the algorithms themselves, which enable one to solve given problems, but also because identification of the collection of structures they most effectively solve can enhance ones ability to formulate problems.
1.2 Types of Problems
The content of this book is divided into three major parts: Linear Programming, Unconstrained Problems, and Constrained Problems. The last two parts together comprise the subject of nonlinear programming.
Linear Programming
Linear programming is without doubt the most natural mechanism for formulating a vast array of problems with modest effort. A linear programming problem is characterized, as the name implies, by linear functions of the unknowns; the objective is linear in the unknowns, and the constraints are linear equalities or linear inequalities in the unknowns. One familiar with other branches of linear mathematics might suspect, initially, that linear programming formulations are popular because the mathematics is nicer, the theory is richer, and the computation simpler for linear problems than for nonlinear ones. But, in fact, these are not the primary reasons. In terms of mathematical and computational properties, there are much broader classes of optimization problems than linear programming problems that have elegant and potent theories and for which effective algorithms are available. It seems that the popularity of linear programming lies primarily with the formulation phase of analysis rather than the solution phaseand for good cause. For one thing, a great number of constraints and objectives that arise in practice are indisputably linear. Thus, for example, if one formulates a problem with a budget constraint restricting the total amount of money to be allocated among two different commodities, the budget constraint takes the form
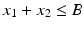
, where x j , i =1,2, is the amount allocated to activity i , and B is the budget. Similarly, if the objective is, for example, maximum weight, then it can be expressed as
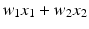
, where w j , i =1,2, is the unit weight of the commodity i . The overall problem would be expressed as
which is an elementary linear program. The linearity of the budget constraint is extremely natural in this case and does not represent simply an approximation to a more general functional form.
Another reason that linear forms for constraints and objectives are so popular in problem formulation is that they are often the least difficult to define. Thus, even if an objective function is not purely linear by virtue of its inherent definition (as in the above example), it is often far easier to define it as being linear than to decide on some other functional form and convince others that the more complex form is the best possible choice. Linearity, therefore, by virtue of its simplicity, often is selected as the easy way out or, when seeking generality, as the only functional form that will be equally applicable (or nonapplicable) in a class of similar problems.
Of course, the theoretical and computational aspects do take on a somewhat special character for linear programming problemsthe most significant development being the simplex method. This algorithm is developed in Chaps.
Unconstrained Problems
It may seem that unconstrained optimization problems are so devoid of structural properties as to preclude their applicability as useful models of meaningful problems. Quite the contrary is true for two reasons. First, it can be argued, quite convincingly, that if the scope of a problem is broadened to the consideration of all relevant decision variables, there may then be no constraintsor put another way, constraints represent artificial delimitations of scope, and when the scope is broadened the constraints vanish. Thus, for example, it may be argued that a budget constraint is not characteristic of a meaningful problem formulation; since by borrowing at some interest rate it is always possible to obtain additional funds, and hence rather than introducing a budget constraint, a term reflecting the cost of funds should be incorporated into the objective. A similar argument applies to constraints describing the availability of other resources which at some cost (however great) could be supplemented.
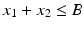 , where x j , i =1,2, is the amount allocated to activity i , and B is the budget. Similarly, if the objective is, for example, maximum weight, then it can be expressed as
, where x j , i =1,2, is the amount allocated to activity i , and B is the budget. Similarly, if the objective is, for example, maximum weight, then it can be expressed as 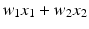 , where w j , i =1,2, is the unit weight of the commodity i . The overall problem would be expressed as
, where w j , i =1,2, is the unit weight of the commodity i . The overall problem would be expressed as