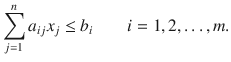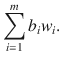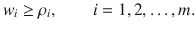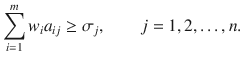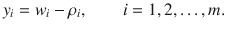This book is mostly about a subject called Linear Programming. Before defining what we mean, in general, by a linear programming problem, let us describe a few practical real-world problems that serve to motivate and at least vaguely to define this subject.
Managing a Production Facility
Consider a production facility for a manufacturing company. The facility is capable of producing a variety of products that, for simplicity, we enumerate as 1,2,, n . These products are constructed/manufactured/produced out of certain raw materials. Suppose that there are m different raw materials, which again we simply enumerate as 1,2,, m . The decisions involved in managing/operating this facility are complicated and arise dynamically as market conditions evolve around it. However, to describe a simple, fairly realistic optimization problem, we consider a particular snapshot of the dynamic evolution. At this specific point in time, the facility has, for each raw material i =1,2,, m , a known amount, say b i , on hand. Furthermore, each raw material has at this moment in time a known unit market value. We denote the unit value of the i th raw material by i .
In addition, each product is made from known amounts of the various raw materials. That is, producing one unit of product j requires a certain known amount, say a ij units, of raw material i . Also, the j th final product can be sold at the known prevailing market price of j dollars per unit.
Throughout this section we make an important assumption:
The production facility is small relative to the market as a whole and therefore cannot through its actions alter the prevailing market value of its raw materials, nor can it affect the prevailing market price for its products.
We consider two optimization problems related to the efficient operation of this facility (later, in , we will see that these two problems are in fact closely related to each other).
1.1 Production Manager as Optimist
The first problem we wish to consider is the one faced by the companys production manager. It is the problem of how to use the raw materials on hand. Let us assume that she decides to produce x j units of the j th product, j =1,2,, n . The revenue associated with the production of one unit of product j is j . But there is also a cost of raw materials that must be considered. The cost of producing one unit of product j is
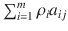
. Therefore, the net revenue associated with the production of one unit is the difference between the revenue and the cost. Since the net revenue plays an important role in our model, we introduce notation for it by setting
Now, the net revenue corresponding to the production of x j units of product j is simply c j x j , and the total net revenue is
The production planners goal is to maximize this quantity. However, there are constraints on the production levels that she can assign. For example, each production quantity x j must be nonnegative, and so she has the constraints
Secondly, she cant produce more product than she has raw material for. The amount of raw material i consumed by a given production schedule is
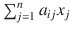
, and so she must adhere to the following constraints:
To summarize, the production managers job is to determine production values x j , j =1,2,, n , so as to maximize (). This optimization problem is an example of a linear programming problem. This particular example is often called the resource allocation problem .
1.2 Comptroller as Pessimist
In another office at the production facility sits an executive called the comptroller. The comptrollers problem (among others) is to assign a value to the raw materials on hand. These values are needed for accounting and planning purposes to determine the cost of inventory . There are rules about how these values can be set. The most important such rule (and the only one relevant to our discussion) is the following:
The company must be willing to sell the raw materials should an outside firm offer to buy them at a price consistent with these values.
Let w i denote the assigned unit value of the i th raw material, i =1,2,, m . That is, these are the numbers that the comptroller must determine. The lost opportunity cost of having b i units of raw material i on hand is b i w i , and so the total lost opportunity cost is
The comptrollers goal is to minimize this lost opportunity cost (to make the financial statements look as good as possible). But again, there are constraints. First of all, each assigned unit value w i must be no less than the prevailing unit market value i , since if it were less an outsider would buy the companys raw material at a price lower than i , contradicting the assumption that i is the prevailing market price. That is,
Similarly,
To see why, suppose that the opposite inequality holds for some specific product j . Then an outsider could buy raw materials from the company, produce product j , and sell it at a lower price than the prevailing market price. This contradicts the assumption that j is the prevailing market price, which cannot be lowered by the actions of the company we are studying. Minimizing () is a linear programming problem. It takes on a slightly simpler form if we make a change of variables by letting
In words, y i is the increase in the unit value of raw material i representing the mark-up the company would charge should it wish simply to act as a reseller and sell raw materials back to the market. In terms of these variables, the comptrollers problem is to minimize
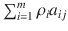 . Therefore, the net revenue associated with the production of one unit is the difference between the revenue and the cost. Since the net revenue plays an important role in our model, we introduce notation for it by setting
. Therefore, the net revenue associated with the production of one unit is the difference between the revenue and the cost. Since the net revenue plays an important role in our model, we introduce notation for it by setting 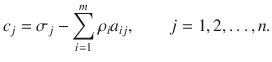
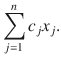

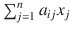 , and so she must adhere to the following constraints:
, and so she must adhere to the following constraints: