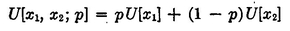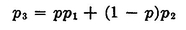Robert Dorfman - Linear Programming and Economic Analysis

In Chap. 14 we saw that strategies that lead to probability distributions rather than to definite numerical pay-offs are essential to the theory of games. Such strategies are fundamental in the solution of nonstrictly determined games, and they turn up elsewhere as well. It is thus necessary for players to be able to evaluate the desirabilities of probability distributions just as they evaluate the desirabilities of definite pay-offs. For this purpose game theory adopts the following postulate: In evaluating the desirabilities of probability distributions of pay-offs players should pay attention exclusively to the expected values of those probability distributions. We do not have to labor the point that the solution of nonstrictly determined games by the use of mixed strategies, the major achievement of game theory, rests squarely on this postulate.

At the same time, this assumption goes against the grain. Everyone knows that there is a lot more to a probability distribution than its expected value, and it seems irresistible intuitively that the reasonable player should take into account other characteristics such as the dispersion, skewness, etc. The purpose of this appendix is to sketch a justification of the postulate.

We can get to the heart of the issue by considering it in its baldest form. Suppose a choice is to be made between these two outcomes: (1) A 50-50 chance of winning or losing $ 10; (2) a 50-50 chance of winning or losing $ 10,000. It would be presumptuous for von Neumann and Morgenstern or anyone else to maintain that because these two outcomes have the same monetary expected value a reasonable man should be indifferent between them, and von Neumann and Morgenstern do not maintain this. They would agree that a man may quite reasonably prefer outcome 1 if he is more fearful of losing so great a sum as $ 10,000 than he is desirous of gaining it. What they do maintain is that a reasonable man need pay attention only to the expected value of the utilities associated with the various outcomes, the so-called moral expectation. To bring out the contrast, let U(x) denote the utility of winning x dollars. Then, in our example, the moral expectation of outcome 1 is U (10) + U (10), and the moral expectation of outcome 2 is U (10,000) + U (10,000). For comparison, the actuarial expectations of the two outcomes are

(10) + (10) = (10,000) + (10,000) = 0

The equality of the actuarial expectations does not preclude the possibility that

U (10) + U (10) > U (10,000) + U (10,000)

in which case outcome 1 should, on the game-theory postulate, be preferred.

These considerations immediately raise numerous questions concerning the numerical measurability of utility and other matters, and we shall have to consider some of them later. For the sake of the argument, though, let us postpone these questions and concede for the moment that meaningful numbers, such as U(x) , can be assigned. It still is not immediately evident that the reasonable man should take account of only the expected value of his moral expectation and should disregard its variance, its skewness, and all the rest. We now demonstrate the reasonableness of this postulate by starting from more immediately appealing assumptions and showing that the game-theory postulate follows from them.

For this argument let us define a gamble to be any situation in which two outcomes are possible and in which the probabilities of the two outcomes are known. We shall denote a gamble by [ x 1, x 2; p ], meaning that the two possible outcomes are x 1 and x 2, that the probability of x 1 is p and the probability of x 2 is 1 p .

As our starting point we take the strong independence axiom, one version of which is: If x 1 is indifferent to y 1 and x 2 is indifferent to y 2, then the gamble [ x 1, x 2; p ] is indifferent to the gamble [ y 1, y 2; p ] irrespective of what the outcomes are and of the value of p. This axiom says merely that if the consequences of two gambles are pairwise indifferent and their probabilities are the same, then there is no reason to prefer one over the other.

Let U [ ] denote the utility or desirability of any situation, be it a definite payment or a gamble. Our task is to show that

(A-1)

whatever x 1, x 2, and p may be, i.e., that the utility of a gamble is equal to the expected value of the utilities of the outcomes. To do this we conceive of a very desirable outcome called M and a very undesirable one called N and consider gambles in which M and N are the stakes. Such gambles, which have the form [ M , N ; p ], will be called standard gambles and will be used to evaluate the desirability of other gambles and of fixed outcomes. We assume (this is really a second axiom) that it is possible to find a standard gamble that is just as desirable as outcome x 1 (i.e., the standard gamble and x 1 are indifferent alternatives). Let this gamble be [ M , N ; p 1]. Clearly, the more desirable x 1, the greater will be p 1, the probability of the favorable outcome in the standard gamble indifferent to x 1.

Similarly let [ M , N ; p 2] be the standard gamble indifferent to x 2 and [ M , N ; p 3] be the standard gamble indifferent to the original gamble [ x 1, x 2; p ]. Then, by the strong-independence axiom, the compound gamble

{[ M, N; p 1], [ M, N; p 2]; p }

is indifferent to the original gamble [ x 1, x ; p]. The compound gamble {[ M, N; p 1], [ M, N; p 2]; p } is a two-stage uncertain event, the outcomes of whose first stage are the ordinary gambles indicated. The classic example of such a compound gamble is the Irish sweepstakes. In the case at hand, p is the probability that the outcome of the initial chance event will be [ M, N; p 1], and p 1 is the probability that M will result from the second stage. Thus the probability of winning M via [ M, N; p 1] is pp 1. Similarly, the probability of winning M via [ M, N; p 2] is (1 p ) p 2, and therefore the total probability of winning M from the compound gamble is pp + (1 p ) p 2. Now notice that the compound gamble has the same ultimate outcomes as [ M, N; p 3], and since they are both indifferent to [ x 1, x 2; p ], they are indifferent to each other. Therefore the probability of winning M must be the same in these two gambles, and

(A-2)

Since the probabilities occurring in standard gambles indicate relative desirability, they can be used as Paretian indexes of ophelimity, or utility. Thus the utility of any situation, say S , is measured by the probability, say p s , of winning M in the standard gamble indifferent to S ; that is, we may write U[S] = p s , where ps , satisfies U[S] = U [ M, N; p s ]. Then p 1 = U [ x 1], p 2 = U [ x 2], p 3 = U [ x 1, x 2; p ]. Substituting these values in Eq. (A-2), Eq. (A-1) results and is proved. This argument generalizes readily to uncertain events with more than two outcomes. The essential assumption on which our argument is founded is worth restating. It is that we can reduce a compound gamble to a simple one via the rules of probability without changing its desirability.

In the course of this argument we answered the question of whether it is possible to assign definite numbers to the desirabilities of different situations. Our answer was that one way of doing this, and of course not the only way, is to measure the utility of any situation by the probability of the favorable outcome in the standard gamble indifferent to it. This procedure will assign higher numbers to more desirable situations and thus fulfill all the requirements of an ordinal utility indicator of the sort conceived by Pareto. Of course, any monotonic function of ps could also serve as an ordinal utility indicator, but only the one we have chosen will have the very handy property expressed in Eq. (A-1) and employed in the theory of games. Thus for purposes of game theory it must be assumed that utility is measured in this way. This is, by the way, an empirically observable measure of utility, arbitrary only up to scale and origin constants as determined by the choice of M and N . A more complete proof would show (1) that the choice of M and N can be arbitrary without really affecting anything, and (2) that the utility indicator can be extended to outcomes worse than M or better than N.