The Theory of LINEARVISCOELASTICITY The Theory of LINEARVISCOELASTICITYD. R. Bland University of Manchester DOVER PUBLICATIONS, INC. Mineola, New York Bibliographical Note This Dover edition, first published in 2016, is an unabridged republication of the work originally published as Vol. 10 in the International Series of Monographs on Pure and Applied Mathematics by Pergamon Press, New York, in 1960. R. (David Russell), author. (David Russell), author.
Title: The theory of linear viscoelasticity / D.R. Bland. Other titles: Linear viscoelasticity Description: Mineola, New York : Dover Publications, Inc., 2016. | This Dover edition, first published in 2016, is an unabridged republication of the work originally published as Vol. 10 in the International Series of Monographs on Pure and Applied Mathematics by Pergamon Press, New York, in 1960Title page verso. | Includes bibliographical references and index.
Identifiers: LCCN 2016015242| ISBN 9780486462691 | ISBN 0486462692 Subjects: LCSH: Elasticity. | Viscosity. Classification: LCC QA931 .B5 2016 | DDC 531/.382dc23 LC record available at https://lccn.loc.gov/2016015242 Manufactured in the United States by RR Donnelley 46269201 2016 www.doverpublications.com CONTENTS CHAPTER 1 MODELSAN INTRODUCTION TO THE CONCEPTS OF VISCOELASTICITY 1.Force-extension equations of the simple models Viscoelasticity, as its name implies, is a generalization of elasticity and viscosity. The ideal linear elastic element is the spring. When a tensile force is applied to it, the increase in distance between its two ends is proportional to the force. The ideal linear viscous element is the dashpot.
It has the property that, when a tensile force is applied to it, the sides move apart at a rate that is proportional to the force. A loose fitting piston in a liquid-filled cylinder, arranged so that liquid flows out around the sides of the piston when it moves slowly up the cylinder, is an example of such an element. The two elements are represented diagrammatically in .  F IG . 1.1.
F IG . 1.1.  F IG. 1.2. 1.2.
F IG. 1.2. 1.2.
The viscous element, the dashpot. If F is the force and a is the extension, i.e. the increase in distance between the ends of the spring in the loaded from the unloaded state, then 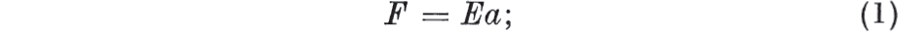 E is a constant, known as the modulus of the spring. For the dashpot, the relationship is
E is a constant, known as the modulus of the spring. For the dashpot, the relationship is 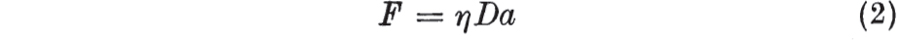 where the operator D denotes differentiation with respect to time; is a constant, known as the viscosity of the dashpot. In viscoelasticity the basic elastic and viscous elements are combined. In this chapter we shall be concerned with networks that are essentially one-dimensional.
where the operator D denotes differentiation with respect to time; is a constant, known as the viscosity of the dashpot. In viscoelasticity the basic elastic and viscous elements are combined. In this chapter we shall be concerned with networks that are essentially one-dimensional.
The elements all lie in the same direction and all the forces concerned act in this direction. In this section some of the simpler combination of elements are considered. The elements can be combined in series. The combination is known as a Maxwell element and is illustrated in . Suppose a tensile force F is applied to this element. 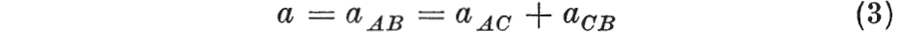 where C is the point of junction of spring and dashpot. aAC is given by ,
where C is the point of junction of spring and dashpot. aAC is given by , 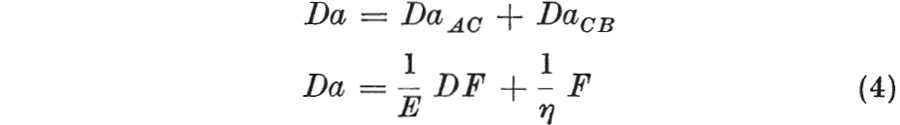 on substituting from is the required relationship between a and F.
on substituting from is the required relationship between a and F. 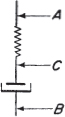 F IG. 1.3. 1.3.
F IG. 1.3. 1.3.
The Maxwell element. 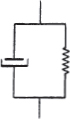 F IG. 1.4. The Voigt element. The combination of the elastic and viscous elements in parallel is known as a Voigt element (sometimes as a Kelvin or KelvinVoigt element) and is illustrated in . The extension a is the same in spring and dashpot.
F IG. 1.4. The Voigt element. The combination of the elastic and viscous elements in parallel is known as a Voigt element (sometimes as a Kelvin or KelvinVoigt element) and is illustrated in . The extension a is the same in spring and dashpot.
If the tensile force in the spring is FS and that in the dashpot FD, then 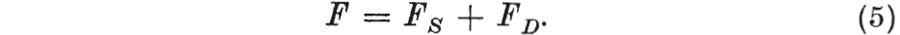 Substituting from ,
Substituting from , 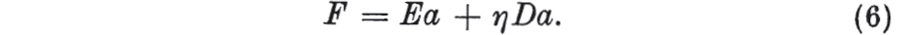 This is the relationship between force and extension for the Voigt element. If E is infinite in . In these special cases the Maxwell and Voigt elements degenerate to the simplest elements. From two springs and one dashpot, two non-degenerate.
This is the relationship between force and extension for the Voigt element. If E is infinite in . In these special cases the Maxwell and Voigt elements degenerate to the simplest elements. From two springs and one dashpot, two non-degenerate. 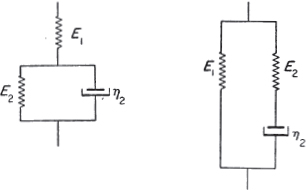 F IG. 1.5.
F IG. 1.5.
Alternative representations of the three-element elastic model. The left-hand model consists of an elastic and a Voigt element in series. The force F is the same in the two elements and the extension a is the sum of the extensions, a1 and a2, in the two elements, i.e. 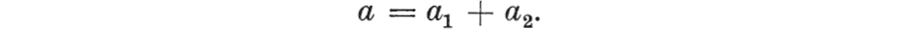 From ,
From , 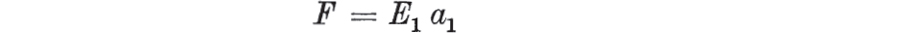 and, from ,
and, from , 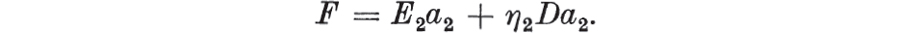 Eliminating a1 and a2,
Eliminating a1 and a2, 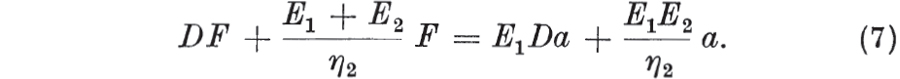 Since an equation is unaltered when multiplied throughout by any non-zero quantity, the coefficient of the highest order derivative of F can be taken as unity. The right-hand model in consists of an elastic and a Maxwell element in parallel. It is left as an exercise for the reader to show that it has a force-extension relationship
Since an equation is unaltered when multiplied throughout by any non-zero quantity, the coefficient of the highest order derivative of F can be taken as unity. The right-hand model in consists of an elastic and a Maxwell element in parallel. It is left as an exercise for the reader to show that it has a force-extension relationship 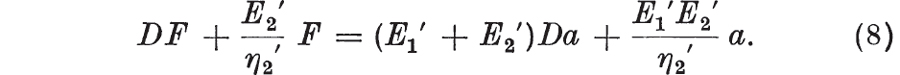 Thus for a given force-extension equation of the form
Thus for a given force-extension equation of the form 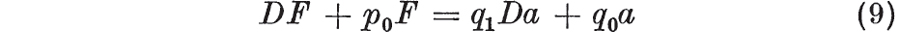 two distinct model representations exist.
two distinct model representations exist.
The elastic and viscous constants of one model are found by equating the coefficients of . The two sets of constants are not the same. In fact whenever the non-degenerate model representation of a particular force-extension equation consists of more than two elements, the model representation is not unique. The reader should now be able to show that two non-degenerate models can be constructed from two dashpots and one spring. Either model is known as the 3-element viscous model and its force-extension equation is of the form 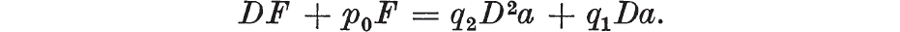 A particularly useful model is that shown in with three more representations equivalent to it. 1.6. 1.6.
A particularly useful model is that shown in with three more representations equivalent to it. 1.6. 1.6.
Next page















 F IG . 1.1.
F IG . 1.1.  F IG. 1.2. 1.2.
F IG. 1.2. 1.2.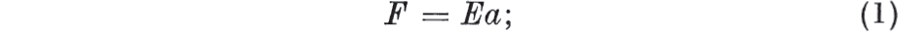 E is a constant, known as the modulus of the spring. For the dashpot, the relationship is
E is a constant, known as the modulus of the spring. For the dashpot, the relationship is 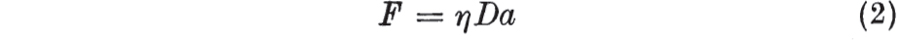 where the operator D denotes differentiation with respect to time; is a constant, known as the viscosity of the dashpot. In viscoelasticity the basic elastic and viscous elements are combined. In this chapter we shall be concerned with networks that are essentially one-dimensional.
where the operator D denotes differentiation with respect to time; is a constant, known as the viscosity of the dashpot. In viscoelasticity the basic elastic and viscous elements are combined. In this chapter we shall be concerned with networks that are essentially one-dimensional.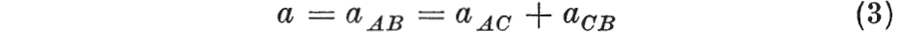 where C is the point of junction of spring and dashpot. aAC is given by ,
where C is the point of junction of spring and dashpot. aAC is given by , 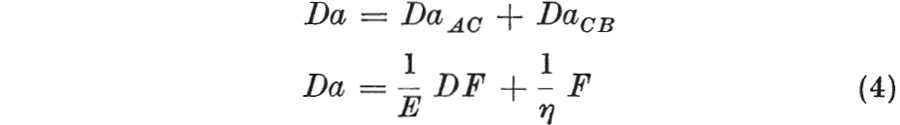 on substituting from is the required relationship between a and F.
on substituting from is the required relationship between a and F.  F IG. 1.3. 1.3.
F IG. 1.3. 1.3. F IG. 1.4. The Voigt element. The combination of the elastic and viscous elements in parallel is known as a Voigt element (sometimes as a Kelvin or KelvinVoigt element) and is illustrated in . The extension a is the same in spring and dashpot.
F IG. 1.4. The Voigt element. The combination of the elastic and viscous elements in parallel is known as a Voigt element (sometimes as a Kelvin or KelvinVoigt element) and is illustrated in . The extension a is the same in spring and dashpot.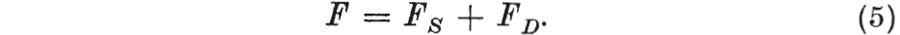 Substituting from ,
Substituting from , 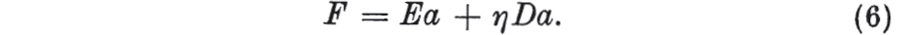 This is the relationship between force and extension for the Voigt element. If E is infinite in . In these special cases the Maxwell and Voigt elements degenerate to the simplest elements. From two springs and one dashpot, two non-degenerate.
This is the relationship between force and extension for the Voigt element. If E is infinite in . In these special cases the Maxwell and Voigt elements degenerate to the simplest elements. From two springs and one dashpot, two non-degenerate.  F IG. 1.5.
F IG. 1.5.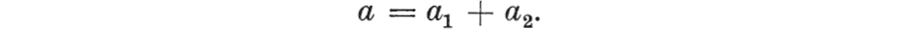 From ,
From , 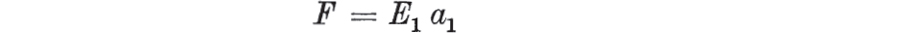 and, from ,
and, from , 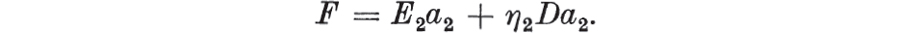 Eliminating a1 and a2,
Eliminating a1 and a2, 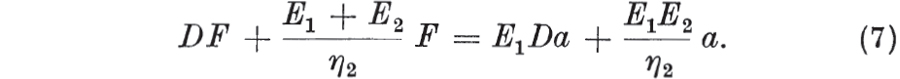 Since an equation is unaltered when multiplied throughout by any non-zero quantity, the coefficient of the highest order derivative of F can be taken as unity. The right-hand model in consists of an elastic and a Maxwell element in parallel. It is left as an exercise for the reader to show that it has a force-extension relationship
Since an equation is unaltered when multiplied throughout by any non-zero quantity, the coefficient of the highest order derivative of F can be taken as unity. The right-hand model in consists of an elastic and a Maxwell element in parallel. It is left as an exercise for the reader to show that it has a force-extension relationship 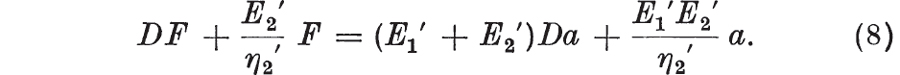 Thus for a given force-extension equation of the form
Thus for a given force-extension equation of the form 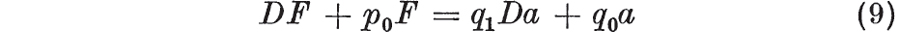 two distinct model representations exist.
two distinct model representations exist.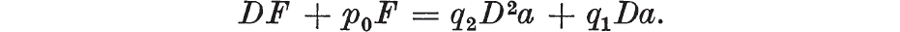 A particularly useful model is that shown in with three more representations equivalent to it. 1.6. 1.6.
A particularly useful model is that shown in with three more representations equivalent to it. 1.6. 1.6.