This introduction to dimensional analysis covers the methods, history, and formalization of the field, and provides physics and engineering applications. Covering topics from mechanics, hydro- and electrodynamics to thermal and quantum physics, it illustrates the possibilities and limitations of dimensional analysis. Introducing basic physics and fluid engineering topics through the mathematical methods of dimensional analysis, this book is perfect for students in physics, engineering, and mathematics. Explaining potentially unfamiliar concepts such as viscosity and diffusivity, this text includes worked examples and end-of-chapter problems with answers provided in an accompanying appendix, which help make this text ideal for self-study. Long-standing methodological problems arising in popular presentations of dimensional analysis are also identified and solved, making it a useful text for advanced students and professionals.
Don S. Lemons is Professor Emeritus of Physics at Bethel College in North Newton, Kansas, and has served as an assistant editor of the American Journal of Physics . He is a member of the American Physical Society and his research focuses primarily on plasma physics.
Don S. Lemons
University Printing House, Cambridge CB2 8BS, United Kingdom
One Liberty Plaza, 20th Floor, New York, NY 10006, USA
477 Williamstown Road, Port Melbourne, VIC 3207, Australia
4843/24, 2nd Floor, Ansari Road, Daryaganj, Delhi 110002, India
79 Anson Road, #0604/06, Singapore 079906
Cambridge University Press is part of the University of Cambridge.
It furthers the Universitys mission by disseminating knowledge in the pursuit of education, learning, and research at the highest international levels of excellence.
www.cambridge.org
Information on this title: www.cambridge.org/9781107161153
10.1017/9781316676165
Don S.Lemons 2017
This publication is in copyright. Subject to statutory exception and to the provisions of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press.
First published 2017
Printed in the United Kingdom by TJ International Ltd. Padstow Cornwall
A catalogue record for this publication is available from the British Library.
Library of Congress Cataloging-in-Publication Data
Names: Lemons, Don S. (Don Stephen), 1949 author.
Title: A students guide to dimensional analysis / Don Lemons.
Description: New York : Cambridge University Press, 2017. | Includes bibliographical references and index.
Identifiers: LCCN 2016040385 | ISBN 9781107161153 (hardback)
Subjects: LCSH: Dimensional analysis. | BISAC: SCIENCE / Mathematical Physics.
Classification: LCC TA347.D5 L46 2017 | DDC 530.8dc23 LC record available at https://lccn.loc.gov/2016040385
ISBN 978-1-107-16115-3 Hardback
ISBN 978-1-316-61381-8 Paperback
Cambridge University Press has no responsibility for the persistence or accuracy of URLs for external or third-party Internet Web sites referred to in this publication and does not guarantee that any content on such Web sites is, or will remain, accurate or appropriate.
Contents
Preface
I was charmed when as a young student I watched one of my physics professors, the late Harold Daw, work a problem with dimensional analysis. The result appeared as if by magic without the effort of constructing a model, solving a differential equation, or applying boundary conditions. But the inspiration of the moment did not, until many years later, bear fruit. In the meantime my acquaintance with this important tool remained partial and superficial. Dimensional analysis seemed to promise more than it could deliver.
Dimensional analysis has charmed and disappointed others as well. Yet there is no doubt that a deep understanding of its methods is useful to researchers in a number of fields. Attesting to this fact is that dimensional analysis is the subject of several good, graduate-level monographs. Even so, dimensional analysis is often ignored at the introductory level except when teachers admonish their students to check the units of their result and warn them against adding apples and oranges.
The problem for teachers and students is that dimensional analysis has no settled place in the physics curriculum. The mathematics required for its application is quite elementary of the kind one learns in a good high school course and its foundational principle is essentially a more precise version of the rule against adding apples and oranges. Yet the successful application of dimensional analysis requires physical intuition an intuition that develops only slowly with the experience of modeling and manipulating physical variables. But how much intuition is required?
I have written A Students Guide to Dimensional Analysis in the belief that the simple techniques of dimensional analysis can deepen our understanding and enhance our exploration of physical situations and processes at the introductory level. Thus, this text is designed for students who are taking or have taken an entry-level, mathematically oriented, university physics course. More experienced students and professionals may also find this text useful.
One elementary application of dimensional analysis is to a simple pendulum, that is, to a compact weight swinging from the end of a string. How long does the pendulum take to complete one cycle of its motion? It seems that this interval t might depend on the mass of the weight m , the acceleration of gravity g , the length of the string l , and the maximum angle of its swing . The adjective simple in simple pendulum means that the size of the weight is negligibly small compared to the length of the pendulum l . Therefore, we search for a function of m , l , g , and that produces t . We note that the International System or SI unit of the period t is the second, the SI unit of mass m is the kilogram, of length l is the meter, and of acceleration g is a meter divided by a second squared. The angle is dimensionless. We quickly discover that 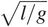 is the only combination of m , l , and g that produces a quantity whose SI unit is a second. Therefore, it must be that
is the only combination of m , l , and g that produces a quantity whose SI unit is a second. Therefore, it must be that
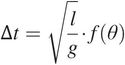
where f () is an as yet undetermined, dimensionless function of .
This result is typical of dimensional analysis. Much is learned but something is left unlearned. The analysis teaches us that the period t of a simple pendulum is directly proportional to the square root of its length 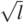 and does not at all depend on its mass m . We could experimentally verify these findings, but dimensional analysis suggests that limited time might be better spent exploring the undetermined function f () . However, this example misleads as well as informs. Not many applications of dimensional analysis are this simple, nor are we usually aware, as we probably are in this case, of the result beforehand.
and does not at all depend on its mass m . We could experimentally verify these findings, but dimensional analysis suggests that limited time might be better spent exploring the undetermined function f () . However, this example misleads as well as informs. Not many applications of dimensional analysis are this simple, nor are we usually aware, as we probably are in this case, of the result beforehand.
Dimensional analysis is most revealing when we know something but not everything about a situation or process. Then dimensional analysis builds on that something we already know. We might, for instance, be familiar with the equations that describe a certain process but not have the skill or the time to solve them in the usual way. Or we might wish to expand our preliminary knowledge of a solution before completely determining its form. Then again, we might know only the category of the problem (that is, mechanics, thermodynamics, or electrodynamics) and the variable we want to determine (that is, an oscillation period, a pressure drop, or an energy loss rate). In all these cases, dimensional analysis constrains how the relevant physical variables and constants work together to produce the result sought.














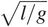 is the only combination of m , l , and g that produces a quantity whose SI unit is a second. Therefore, it must be that
is the only combination of m , l , and g that produces a quantity whose SI unit is a second. Therefore, it must be that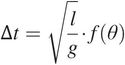
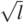 and does not at all depend on its mass m . We could experimentally verify these findings, but dimensional analysis suggests that limited time might be better spent exploring the undetermined function f () . However, this example misleads as well as informs. Not many applications of dimensional analysis are this simple, nor are we usually aware, as we probably are in this case, of the result beforehand.
and does not at all depend on its mass m . We could experimentally verify these findings, but dimensional analysis suggests that limited time might be better spent exploring the undetermined function f () . However, this example misleads as well as informs. Not many applications of dimensional analysis are this simple, nor are we usually aware, as we probably are in this case, of the result beforehand.