Student Solutions Manual for Nonlinear Dynamics and Chaos, Second EditionMitchal Dichter First published 2017 by Westview Press Published 2018 by CRC Press Taylor & Francis Group 6000 Broken Sound Parkway NW, Suite 300 Boca Raton, FL 33487-2742 CRC Press is an imprint of the Taylor & Francis Group, an informa business Copyright 2017 by Steven H. Strogatz and Taylor & Francis Group LLC No claim to original U.S. Government works This book contains information obtained from authentic and highly regarded sources. Reasonable efforts have been made to publish reliable data and information, but the author and publisher cannot assume responsibility for the validity of all materials or the consequences of their use. The authors and publishers have attempted to trace the copyright holders of all material reproduced in this publication and apologize to copyright holders if permission to publish in this form has not been obtained. If any copyright material has not been acknowledged please write and let us know so we may rectify in any future reprint.
First published 2017 by Westview Press Published 2018 by CRC Press Taylor & Francis Group 6000 Broken Sound Parkway NW, Suite 300 Boca Raton, FL 33487-2742 CRC Press is an imprint of the Taylor & Francis Group, an informa business Copyright 2017 by Steven H. Strogatz and Taylor & Francis Group LLC No claim to original U.S. Government works This book contains information obtained from authentic and highly regarded sources. Reasonable efforts have been made to publish reliable data and information, but the author and publisher cannot assume responsibility for the validity of all materials or the consequences of their use. The authors and publishers have attempted to trace the copyright holders of all material reproduced in this publication and apologize to copyright holders if permission to publish in this form has not been obtained. If any copyright material has not been acknowledged please write and let us know so we may rectify in any future reprint.
Except as permitted under U.S. Copyright Law, no part of this book may be reprinted, reproduced, transmitted, or utilized in any form by any electronic, mechanical, or other means, now known or hereafter invented, including photocopying, microfilming, and recording, or in any information storage or retrieval system, without written permission from the publishers. For permission to photocopy or use material electronically from this work, please access www.copyright.com (http://www.copyright.com/) or contact the Copyright Clearance Center, Inc. (CCC), 222 Rosewood Drive, Danvers, MA 01923, 978-750-8400. CCC is a not-for-profit organization that provides licenses and registration for a variety of users. For organizations that have been granted a photocopy license by the CCC, a separate system of payment has been arranged.
Trademark Notice: Product or corporate names may be trademarks or registered trademarks, and are used only for identification and explanation without intent to infringe. Visit the Taylor & Francis Web site at
http://www.taylorandfrancis.com and the CRC Press Web site at http://www.crcpress.com Every effort has been made to secure required permissions for all text, images, maps, and other art reprinted in this volume. A CIP catalog record for the print version of this book is available from the Library of Congress ISBN 13: 978-0-8133-5054-7 (pbk) CONTENTS2.1.1 The fixed points of the flow x=sin(x) occur when x=0sin(x)=0x=zz 2.1.3 a) We can find the flows acceleration by first deriving an equation containing by taking the time derivative of the differential equation. ddtx=ddtsin(x)x=cos(x)x We can obtain solely as a function of x by plugging in our previous equation for . x=cos(x)sin(x) b) We can find what values of x give the acceleration maximum positive values by using the trigonometric identity 12sin(2x)=sin(x)cos(x) which can be used to rewrite as x=12sin(2x) which has maximums when x=(z+14)z 2.1.5 a) A pendulum submerged in honey with the pendulum at the 12 oclock position corresponding to x = 0 is qualitatively similar to = sin(x). b) x = 0 and x = being unstable and stable fixed points respectively is consistent with our intuitive understanding of gravity. 2.2.1 x=4x216 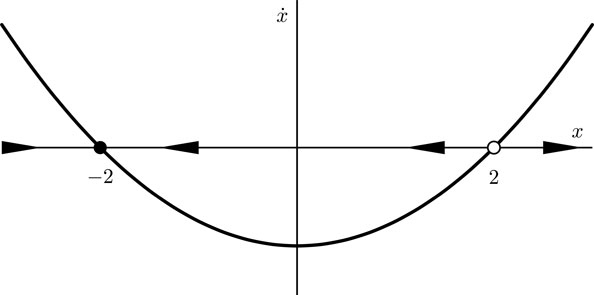
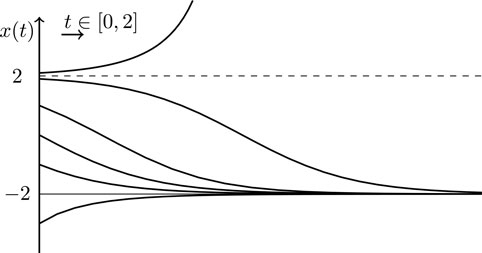 x(t)=2(x0e16t+x02e16t+2)x0e16t+x0+2e16t+2 2.2.3 x=xx3
x(t)=2(x0e16t+x02e16t+2)x0e16t+x0+2e16t+2 2.2.3 x=xx3 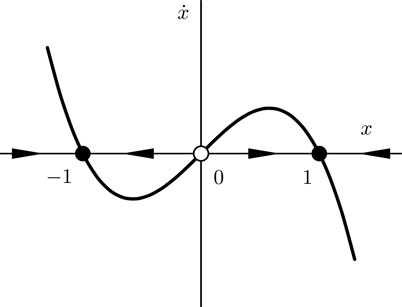
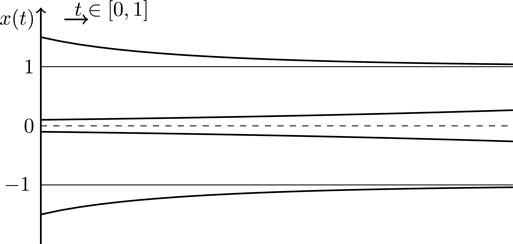 x(t)=et11x02+e2t1dependingonthesignoftheinitialcondition. 2.2.5 x=1+12cos(x)
x(t)=et11x02+e2t1dependingonthesignoftheinitialcondition. 2.2.5 x=1+12cos(x) 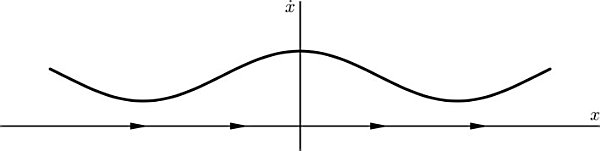 There are no fixed points, but the rate increase for x(t) does vary.
There are no fixed points, but the rate increase for x(t) does vary. 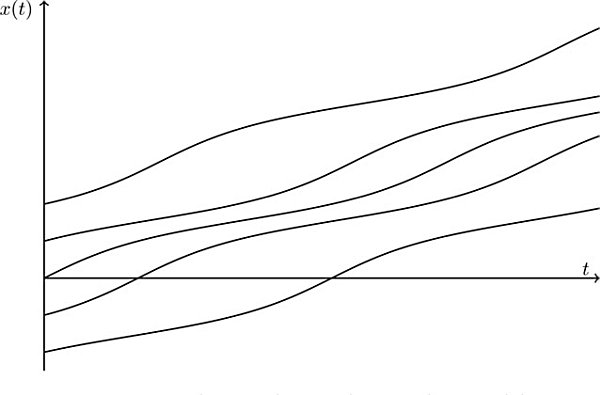 x(t)=2arctan(3tan(arctan(tan(x02)3)+3t4)) 2.2.7 x=excos(x) We cant solve for the fixed points analytically, but we can find the fixed points approximately by looking at the intersections of ex and cos(x), and determine the stability of the fixed points from which graph is greater than the other nearby.
x(t)=2arctan(3tan(arctan(tan(x02)3)+3t4)) 2.2.7 x=excos(x) We cant solve for the fixed points analytically, but we can find the fixed points approximately by looking at the intersections of ex and cos(x), and determine the stability of the fixed points from which graph is greater than the other nearby. 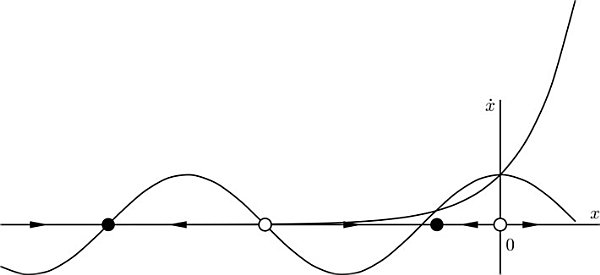 We could also plot the graph using a computer.
We could also plot the graph using a computer. 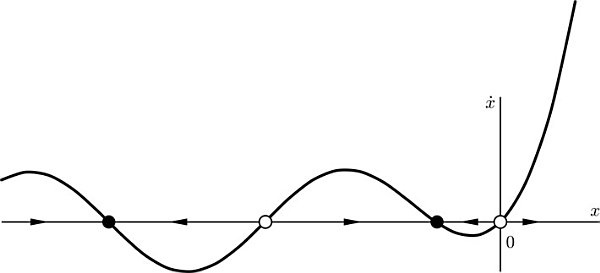 There are fixed points at x(12n), n, and x = 0.
There are fixed points at x(12n), n, and x = 0.  Unable to find an analytic solution. 2.2.9 f(x)=x(x1)
Unable to find an analytic solution. 2.2.9 f(x)=x(x1) 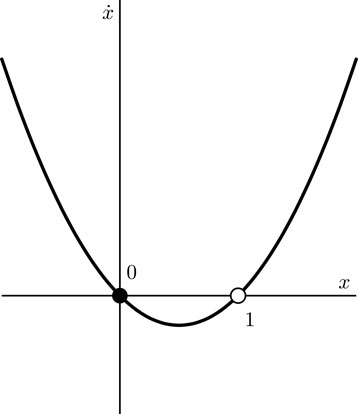 2.2.11 RC circuit Q=V0RQRCQ+1RCQ=V0RQ(0)=0 Multiply by an integrating factor etRC to both sides. 2.2.9 f(x)=x(x1)
2.2.11 RC circuit Q=V0RQRCQ+1RCQ=V0RQ(0)=0 Multiply by an integrating factor etRC to both sides. 2.2.9 f(x)=x(x1)  2.2.11 RC circuit Q=V0RQRCQ+1RCQ=V0RQ(0)=0 Multiply by an integrating factor etRC to both sides.
2.2.11 RC circuit Q=V0RQRCQ+1RCQ=V0RQ(0)=0 Multiply by an integrating factor etRC to both sides.
QetRC+1RCetRCQ=V0RetRCddt(QetRC)=V0RetRC Apply an indefinite integral to both sides with respect to t. ddt(QetRC)dt=V0RetRCdtQetRC=V0CetRC+DQ(t)=V0C+DetRC And using the initial condition. Q(0)=V0C+D=0D=V0CQ(t)=V0C(1etRC) 2.2.13 Terminal velocity The velocity v(t) of a skydiver falling follows the equation mv=mgkv2 with m the mass of the skydiver, g the acceleration due to gravity, and k > 0 the drag coefficient. a) v(t)=mgktanh(gkmt) b) v(t)tmgk c) The terminal velocity should occur at a fixed point. The fixed point occurs when v=0mgkv2=0v=mgk d) vavg=31400ft2100ft116sec253ftsec e) s(t)=mkln(cosh(gkmt)) which can be rewritten using V=mgk into s(t)=V2gln(cosh(gVt)) Using s(116sec) = 29300ft and g=32.2ftsec2 gives 29300ft=V232.2ftsec2ln(cosh(32.2ftsec2Vt)) which can be solved numerically to give V266ftsec. rN(1NK)=rNrN2K=rKNrN2K=rK(KNN2)N=dNdt=rK(KNrN2)dNKNN2=rKdt1KNN2=1KN1K(NK)dNKNN2=dNKNdNK(NK)=1Kln(N)1Kln(NK)=rKdt=rKt+C1Kln(N)1Kln(NK)=rKt+Cln(N)ln(NK)=rt+KCln(NNK)=rt+KCln(NNK)=ln(NKN)=ln(1KN)=rtKC1KN=ertKC=eKCert1eKCert=KNN(t)=K1eKCertN(0)=K1eKC=N0eKC=1KN0N(t)=K1(1KN0)ert b) Making the change of variables x=1N. rN(1NK)=rNrN2K=rKNrN2K=rK(KNN2)N=dNdt=rK(KNrN2)dNKNN2=rKdt1KNN2=1KN1K(NK)dNKNN2=dNKNdNK(NK)=1Kln(N)1Kln(NK)=rKdt=rKt+C1Kln(N)1Kln(NK)=rKt+Cln(N)ln(NK)=rt+KCln(NNK)=rt+KCln(NNK)=ln(NKN)=ln(1KN)=rtKC1KN=ertKC=eKCert1eKCert=KNN(t)=K1eKCertN(0)=K1eKC=N0eKC=1KN0N(t)=K1(1KN0)ert b) Making the change of variables x=1N.
N=1xN=xx2=r1x(11xK)x=rKrxx(t)=Cert+1K1N(t)=Cert+1K=KCert+1KN(t)=KKCert+1N(0)=N0N(t)=K1(1KN0)ert 2.3.3 Tumor growth N=aNln(bN) a) a can be interpreted as specifying how fast the tumor grows, and 1b specifies the stable size of the tumor. b) 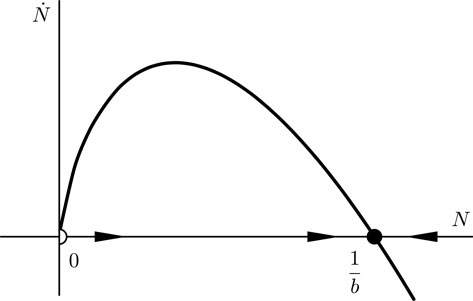
Next page










 First published 2017 by Westview Press Published 2018 by CRC Press Taylor & Francis Group 6000 Broken Sound Parkway NW, Suite 300 Boca Raton, FL 33487-2742 CRC Press is an imprint of the Taylor & Francis Group, an informa business Copyright 2017 by Steven H. Strogatz and Taylor & Francis Group LLC No claim to original U.S. Government works This book contains information obtained from authentic and highly regarded sources. Reasonable efforts have been made to publish reliable data and information, but the author and publisher cannot assume responsibility for the validity of all materials or the consequences of their use. The authors and publishers have attempted to trace the copyright holders of all material reproduced in this publication and apologize to copyright holders if permission to publish in this form has not been obtained. If any copyright material has not been acknowledged please write and let us know so we may rectify in any future reprint.
First published 2017 by Westview Press Published 2018 by CRC Press Taylor & Francis Group 6000 Broken Sound Parkway NW, Suite 300 Boca Raton, FL 33487-2742 CRC Press is an imprint of the Taylor & Francis Group, an informa business Copyright 2017 by Steven H. Strogatz and Taylor & Francis Group LLC No claim to original U.S. Government works This book contains information obtained from authentic and highly regarded sources. Reasonable efforts have been made to publish reliable data and information, but the author and publisher cannot assume responsibility for the validity of all materials or the consequences of their use. The authors and publishers have attempted to trace the copyright holders of all material reproduced in this publication and apologize to copyright holders if permission to publish in this form has not been obtained. If any copyright material has not been acknowledged please write and let us know so we may rectify in any future reprint.
 x(t)=2(x0e16t+x02e16t+2)x0e16t+x0+2e16t+2 2.2.3 x=xx3
x(t)=2(x0e16t+x02e16t+2)x0e16t+x0+2e16t+2 2.2.3 x=xx3 
 x(t)=et11x02+e2t1dependingonthesignoftheinitialcondition. 2.2.5 x=1+12cos(x)
x(t)=et11x02+e2t1dependingonthesignoftheinitialcondition. 2.2.5 x=1+12cos(x)  There are no fixed points, but the rate increase for x(t) does vary.
There are no fixed points, but the rate increase for x(t) does vary.  x(t)=2arctan(3tan(arctan(tan(x02)3)+3t4)) 2.2.7 x=excos(x) We cant solve for the fixed points analytically, but we can find the fixed points approximately by looking at the intersections of ex and cos(x), and determine the stability of the fixed points from which graph is greater than the other nearby.
x(t)=2arctan(3tan(arctan(tan(x02)3)+3t4)) 2.2.7 x=excos(x) We cant solve for the fixed points analytically, but we can find the fixed points approximately by looking at the intersections of ex and cos(x), and determine the stability of the fixed points from which graph is greater than the other nearby.  We could also plot the graph using a computer.
We could also plot the graph using a computer.  There are fixed points at x(12n), n, and x = 0.
There are fixed points at x(12n), n, and x = 0.  Unable to find an analytic solution. 2.2.9 f(x)=x(x1)
Unable to find an analytic solution. 2.2.9 f(x)=x(x1)  2.2.11 RC circuit Q=V0RQRCQ+1RCQ=V0RQ(0)=0 Multiply by an integrating factor etRC to both sides. 2.2.9 f(x)=x(x1)
2.2.11 RC circuit Q=V0RQRCQ+1RCQ=V0RQ(0)=0 Multiply by an integrating factor etRC to both sides. 2.2.9 f(x)=x(x1) 