Peter B. Kahn - Nonlinear Dynamics: Exploration Through Normal Forms

P ROFESSOR E MERITUS

D EPARTMENT OF P HYSICS AND A STRONOMY

S TONY B ROOK U NIVERSITY

P ROFESSOR E MERITUS

J ACOB B LAUSTEIN I NSTITUTES FOR D ESERT R ESEARCH

B EN -G URION U NIVERSITY OF THE N EGEV

Copyright
Copyright 1998, 2014 by Peter B. Kahn and Yair Zarmi
All rights reserved.

Bibliographical Note

This Dover edition, first published in 2014, is an unabridged and corrected republication of the edition originally published in the Wiley Series in Nonlinear Science by John Wiley & Sons, Inc., New York, in 1998.

Library of Congress Cataloging-in-Publication Data

Kahn, Peter B., author.

Nonlinear dynamics : exploration through normal forms / Peter B. Kahn (Professor Emeritus, Department of Physics and Astronomy, Stony Brook University), Yair Zarmi (Professor Emeritus, Jacob Blaustein Institutes for Desert Research, Ben-Gurion University of the Negev). Dover edition.

pages cm

... an unabridged and corrected republication of the edition originally published in the Wiley Series in Nonlinear Science by John Wiley & Sons, Inc., New York, in 1998Title page verso.

Includes bibliographical references and index.

eISBN-13: 978-0-486-79502-7

1. Dynamics. 2. Nonlinear theories. 3. Normal forms (Mathematics) I. Zarmi, Yair, 1942 author. II. Title.

QA845.K34 2014

531.11dc23

2014005677

Manufactured in the United States by Courier Corporation
78045701 2014
www.doverpublications.com

As soon as one starts thinking about nonlinear dynamics, the richness of the subject emerges. It encompasses almost all not linear phenomena and investigators have an enormous range of subject material from which to choose the focus of their investigation. It has been a field of particularly intense study in recent years, due, in great part, to the availability of modern computers and computer software. Many books have been written and there are now journals dedicated to the subject.

With these thoughts in mind, we have come to write this book to bring together a variety of ideas that we have developed in our investigations of a small portion of nonlinear dynamics. In the text, we have concentrated on constructing an exposition of the method of normal forms and its application to ordinary differential equations through perturbation analysis. In particular, we use the inherent freedom in the expansion to obtain expressions that are compact and have computational advantages, as is illustrated in a variety of applications.

The text begins, in , with the a prologue that introduces basic ideas associated with perturbation methods as applied to problems in nonlinear dynamics, particularly the idea of a near-identity transformation and the role it plays in the normal form expansion.

is concerned with establishing error estimates and a discussion of the time-validity of the perturbation expansions that we develop. We introduce some fundamental theorems in dynamical system analysis (i.e., the PoincarLyapunov and the HartmanGrobman theorems) as well as Gronwalls lemma, which is an essential tool in the estimation of and in the finding of bounds for errors in perturbative approximation schemes.

In structure of a finite number of terms in the expansion and not of the full solution. [In our expansions secular or aperiodic terms are those that appear as products of powers of the time multiplied by a trigonometric function. For example, such terms are t sin(t) or t2 sin(t). We will encounter them as genuine and spurious terms in expansions. Illustrative examples are given.]

In , we develop the formalism of the perturbation expansion associated with the method of normal forms. We introduce the fundamental theorems of Poincar and PoincarDulac and address particular attention to the concept of resonance and where the eigenvalues of the unperturbed problem lie in the complex plane. This is followed by a systematic development of the method of normal forms and a detailed discussion of the concept of freedom of choice. We introduce the Duffing oscillator to illustrate various aspects of the normal form expansion and to show explicitly how one computes various terms.

In , we discuss problems in which the eigenvalues of the unperturbed system have negative real part. We learn that, for such problems, naive perturbation theory yields a perturbation expansion that is equivalent to the normal form expansion. This result follows, since it turns out that only a finite number of so-called resonant terms are possible and, as a result, the generators of the expansion can be taken to be the unperturbed solutions. Then, it is a matter of taste (or convenience) which method is employed. We also discuss aspects of finite-time blowup that lead to finite-time validity of the perturbation expansion. In such problems, the perturbation expansion is more correctly a formal transformation since, even if one writes it as a closed-form expression, the expansion is valid only for times less than the blowup time.

In we use the freedom to renormalize the expansion to obtain a very simple way to view the onset of limit cycle oscillations.

In we consider a rich variety of nonautonomous systems. These systems arise naturally when one considers forced linear and nonlinear oscillatory motion such as arises, for instance, in a discussion of the linear and nonlinear Mathieu equations, the study of pendula, orbits in celestial mechanics, electric circuits, nuclear magnetic resonance and for resonant oscillations of charged particles due to multipole errors in guiding magnetic fields in particle accelerators. Here one encounters and identifies real and spurious explosive instabilities. Also, one finds that true secular behavior is possible for nonautonomous systems. We analyze nonautonomous weakly nonlinear oscillatory systems with periodic forcing of the general type

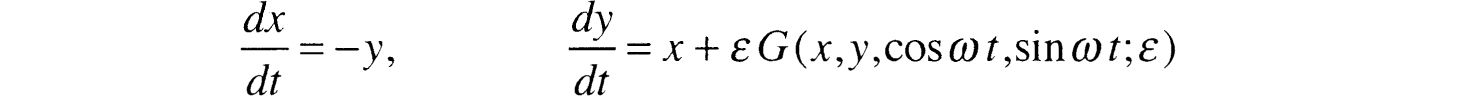
We view cos t and sin t (of which at least one appears in the equations explicitly) as the coordinates of an additional, spurious, harmonic oscillator, treated on equal footing with the position x and the velocity y of the original problem. This increases the dimension of our system from 2 to 4, as is seen from the resulting equations

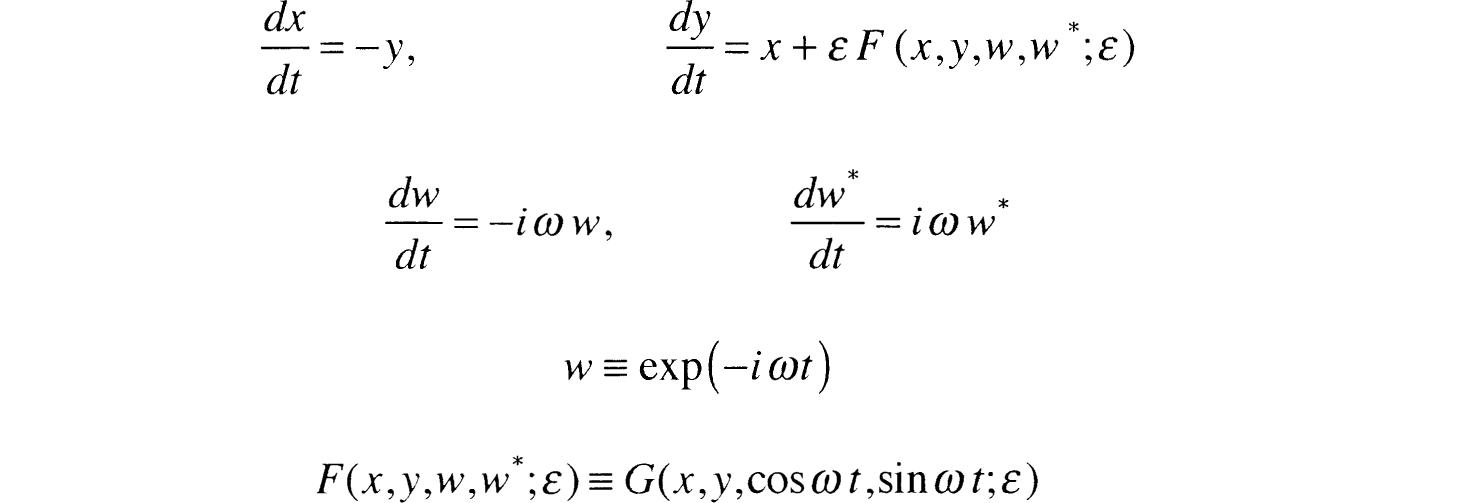
Here x, y, w, w* are scalar variables, F is a scalar forcing function, and 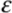is a small parameter. Note that the harmonic time dependence, present in the forcing function, is represented by the variables w, w*. This apparent complication works to our advantage in the normal form analysis as will become evident in the discussion.

is devoted to a discussion of techniques for the treatment of problems in which the unperturbed part has one or more zero eigenvalues and the remaining ones have negative real part. One finds that the method of normal forms, without modification, provides a faithful characterization of such systems. (Specifically, it is easy to accommodate both the transient behavior and finite initial amplitudes within the standard normal form analysis.) For problems of this class, some investigators have found the