Ren Schoof Universitext Catalan's Conjecture 10.1007/978-1-84800-185-5_1 Springer-Verlag London Limited 2008
1. Introduction
In this book, we present Preda Mihilescus beautiful proof of the conjecture made by Eugne Charles Catalan in 1844 in a letter [11] to the editor of Crelles journal:
Je vous prie, Monsieur, de vouloir bien noncer, dans votre recueil, le thorme suivant, que je crois vrai, bien que je naie pas encore russi le dmontrer compltement: dautres seront peut-tre plus heureux:
Deux nombres entiers conscutifs, autres que 8 et 9 ne peuvent tre des puissances exactes; autrement dit: lquation
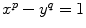
dans laquelle les inconnues sont entires et positives, nadmt quune seule solution.
In other words, Catalan proposed the following.
Conjecture
(E. Catalan, 1844) The only two consecutive numbers in the sequence of perfect powers of natural numbers
are 8 and 9.
When
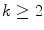
is fixed, the k th powers of natural numbers are necessarily far apart. However, when one varies k , two powers can be closer to one another than one might expect. For instance, we have
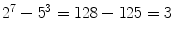
and
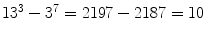
. Catalan conjectured that the only powers for which the difference is as small as 1 are 32 and 23.
Phrased in yet another way, Catalan conjectured that for exponents
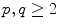
, the Diophantine equation
admits no solution in natural numbers other than the one given by x =3, p =2 and y =2,
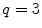
.
Apparently, Catalan himself did not get very far in solving the problem. We read this in a note [12] that was published more than forty years after his 1844 letter. Here Catalan reports on his early attempts:
Aprs avoir perdu prs dune anne la recherche dune dmonstration qui fuyait toujours, jabandonnerai cette recherche fatigante.
The Socit Belge des Professeurs de Mathmatique dExpression Franaise has published a book on the academic and political activities of Eugne Catalan [20]. It contains a reproduction of a painting of Catalan which is at present in the possession of the Universit de Lige (Fig. ).
Fig. 1.1
Eugne Catalan (18141894)
In this book, we mainly concentrate on Preda Mihilescus proof of Catalans famous conjecture. We discuss earlier work only when it is relevant to our presentation of the proof. For an overview of earlier work on the conjecture, see [7, 14, 15, 35, 38]. We only mention one important result: In 1976, Rob Tijdeman [49] (Fig. ) showed that there exist only finitely many pairs of consecutive perfect powers. His proof is based on the theory of linear forms in logarithms. Unfortunately, the bound on the size of the solutions that came out of Tijdemans proof is astronomical. There remained a large gap between the relatively small exponents p,q for which Catalans equation had been solved and Tijdemans estimates. In the successive years, this gap was narrowed considerably by various people [2, 6, 17, 19, 26, 32, 33, 34, 44, 46]. But the gap remained very large. In 1999, refinements of Tijdemans estimates were shown to imply Catalans conjecture when both exponents p,q exceed
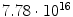
. On the other hand, elaborate computer calculations had proven the conjecture when one of p,q is smaller than 105. See [34] for more information.
Fig. 1.2
Rob Tijdeman. (Reproduced by the kind permission of Rob Tijdeman.)
Between 2000 and 2003, Preda Mihilescu (Fig. ) proved three theorems concerning Catalans conjecture:
Fig. 1.3
Preda Mihilescu. (Reproduced by the kind permission of Robert Tichy.)
Let p,q be odd primes and suppose that x,y are nonzero integers for which
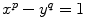
.
Theorem I
(P. Mihilescu, 2000) We have
Theorem II
(P. Mihilescu, 2002) We have
Theorem III
(P. Mihilescu, 2003) We have
Mihilescus proofs of Theorems I, II, and III appear in [35], [36], and [37], respectively. We show now that these three theorems together lead to a proof of Catalans conjecture. This proof does not rely on Tijdemans work or on the computer calculations mentioned above.
Main theorem
The only solutions of the equation
in integers
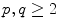
and nonzero integers x, y are given by p =2,
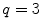
and
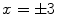
, y =2.
Proof
It is indeed true that
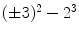
is equal to 1. To prove that there are no other solutions, it suffices to show that there are no other solutions when the exponents p and q are prime numbers . See Exercise 1.1.
The case q =3 was taken care of by V. Lebesgue [27] in 1850. The case p =2 was dealt with by Ko Chao [21] in 1965. See and 3 for detailed proofs of these two results.













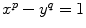 dans laquelle les inconnues sont entires et positives, nadmt quune seule solution.
dans laquelle les inconnues sont entires et positives, nadmt quune seule solution.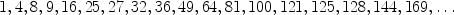
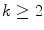 is fixed, the k th powers of natural numbers are necessarily far apart. However, when one varies k , two powers can be closer to one another than one might expect. For instance, we have
is fixed, the k th powers of natural numbers are necessarily far apart. However, when one varies k , two powers can be closer to one another than one might expect. For instance, we have 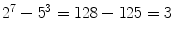 and
and 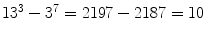 . Catalan conjectured that the only powers for which the difference is as small as 1 are 32 and 23.
. Catalan conjectured that the only powers for which the difference is as small as 1 are 32 and 23.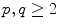 , the Diophantine equation
, the Diophantine equation 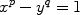
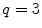 .
.
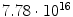 . On the other hand, elaborate computer calculations had proven the conjecture when one of p,q is smaller than 105. See [34] for more information.
. On the other hand, elaborate computer calculations had proven the conjecture when one of p,q is smaller than 105. See [34] for more information. 

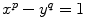 .
.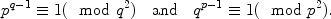
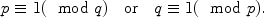
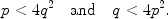
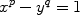
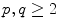 and nonzero integers x, y are given by p =2,
and nonzero integers x, y are given by p =2, 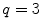 and
and 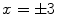 , y =2.
, y =2.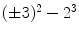 is equal to 1. To prove that there are no other solutions, it suffices to show that there are no other solutions when the exponents p and q are prime numbers . See Exercise 1.1.
is equal to 1. To prove that there are no other solutions, it suffices to show that there are no other solutions when the exponents p and q are prime numbers . See Exercise 1.1.