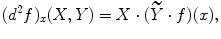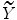• Complain
LitArk » Books » Home and family

Michèle Audin Mihai Damian - Morse Theory and Floer Homology

Here you can read online Michèle Audin Mihai Damian - Morse Theory and Floer Homology full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2013, publisher: Springer, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:

Romance novel Science fiction Adventure Detective Science History Home and family Prose Art Politics Computer Non-fiction Religion Business Children Humor

Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.

Michèle Audin Mihai Damian Morse Theory and Floer Homology

Morse Theory and Floer Homology: summary, description and annotation

We offer to read an annotation, description, summary or preface (depends on what the author of the book "Morse Theory and Floer Homology" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.

This book is an introduction to modern methods of symplectic topology. It is devoted to explaining the solution of an important problem originating from classical mechanics: the Arnold conjecture, which asserts that the number of 1-periodic trajectories of a non-degenerate Hamiltonian system is bounded below by the dimension of the homology of the underlying manifold.

The first part is a thorough introduction to Morse theory, a fundamental tool of differential topology. It defines the Morse complex and the Morse homology, and develops some of their applications.

Morse homology also serves a simple model for Floer homology, which is covered in the second part. Floer homology is an infinite-dimensional analogue of Morse homology. Its involvement has been crucial in the recent achievements in symplectic geometry and in particular in the proof of the Arnold conjecture. The building blocks of Floer homology are more intricate and imply the use of more sophisticated analytical methods, all of which are explained in this second part.

The three appendices present a few prerequisites in differential geometry, algebraic topology and analysis.

The book originated in a graduate course given at Strasbourg University, and contains a large range of figures and exercises. Morse Theory and Floer Homology will be particularly helpful for graduate and postgraduate students.

Michèle Audin Mihai Damian: author's other books


Who wrote Morse Theory and Floer Homology? Find out the surname, the name of the author of the book and a list of all author's works by series.


Michèle Audin Mihai Damian - Morse Theory and Floer Homology
Morse Theory and Floer Homology
Michèle Audin Mihai Damian
Morse Theory and Floer Homology

Morse Theory and Floer Homology — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Morse Theory and Floer Homology" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓
↑
Reset

Interval:

↓
↑

Bookmark:

Make
1234567...213
Part 1
Morse Theory
Michle Audin and Mihai Damian Universitext Morse Theory and Floer Homology 2014 10.1007/978-1-4471-5496-9 Springer-Verlag London 2014
Introduction to Part I
This first part is devoted to Morse theory, with as its main objective the complex defined by the critical points of a Morse function and the trajectories of a gradient field.
It is a theory whose very first building block is the remark that studying a (well-chosen) function can give rather precise information on the topology of a manifold. The most classic examplethese are often also the most instructive onesis that of the height function R 3 R and its restriction to the different submanifolds represented in Figures . In the three cases we consider, the function f is the restriction of .
Fig 1 The round sphere The first figure Figure represents the round - photo 1
Fig. 1
The round sphere
The first figure (Figure ) represents the round sphere, that is, the unit sphere
The level sets f 1 a are Moving upward along the values of the function we - photo 2
The level sets f 1( a ) are
Moving upward along the values of the function we note that the level sets all - photo 3
Moving upward along the values of the function, we note that the level sets all have the same topology until we meet an accident where the topology changes and subsequently remains the same until the next accident.
The same holds for the sublevel sets, that is, what lies below a given level. These are first empty, then (briefly) one point, then a disk, and finally the whole sphere.
The accidents are the critical values of the function, which correspond to the critical points, those where the differential of f is zero, where the tangent plane is horizontal, the north and south poles of the sphere. Of course, the south pole is the minimum of the function and the north pole is its maximum.
The situation is analogous for the torus in the next figure (Figure ), except that there are now critical points that are not extrema of the function, namely the two saddle points. The corresponding level sets are curves in the form of an eight (one is traced in the figure), and are therefore not submanifolds. The regular, noncritical level sets must all be submanifolds because of the submersion theorem.
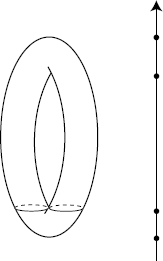
Fig 2 The torus One of the first results of this theory is a theorem due to - photo 4
Fig. 2
The torus
One of the first results of this theory is a theorem due to Reeb (at least for Morse functions). We will prove it in this context. It asserts that a compact manifold on which there exists a function with only two critical points is homeomorphic to a sphere. Of course, there are also functions on the sphere with more critical points.
The third figure (Figure ) is included to illustrate this. Since it is easy to visualize, we have kept the same height function and made a dent in the sphere. Consequently, the submanifold is obviously still diffeomorphic to a sphere, but the function now has two local maxima and a saddle point. Note that the parity of the number of critical points of the new function is the same as that of the original one. If we assume that they are nondegenerate (an important property that will be defined later (and that is satisfied by the critical points in our figures)), then modulo 2 the number of critical points equals the Euler characteristic of the manifold, an invariant that does not depend on the function but only on the manifold.
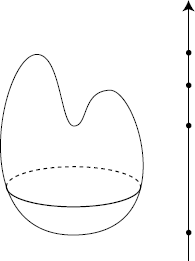
Fig 3 A different sphere The concept of Witten spaces of trajectories - photo 5
Fig. 3
A different sphere
The concept of Witten spaces of trajectories allows us to present a finer invariant. It is clear that the torus and sphere are very different manifolds even if the two admit a function with four nondegenerate critical points. This invariant is what is nowadays called the Morse homology HM k ( V ) of the manifold. It is the homology of a complex, the Morse complex, constructed from the critical points of a Morse function by counting its trajectories along a vector field that connects them These trajectories are those of the gradient of the function (with respect to some metric). In the case of the height function (and the Euclidean metric) one could think of the trajectories of water drops flowing on the surface from one critical point to another. Ultimately, this homology depends only on the (diffeomorphism type of the) manifold. The remarks we just made concerning the number of critical points on such and such manifold can be expressed in the famous Morse inequalities: the number c k of critical points of index k of a Morse function on a manifold satisfies
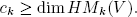
Morse Theory and Floer Homology - image 6
It is therefore natural for these objects to be the subject of the first part of this book.
Michle Audin and Mihai Damian Universitext Morse Theory and Floer Homology 2014 10.1007/978-1-4471-5496-9_1
Springer-Verlag London 2014
1. Morse Functions
Michle Audin 1 and Mihai Damian 1
(1)
IRMA, Universit Louis Pasteur, Strasbourg Cedex, France
Abstract
We define Morse functions and prove the basic results (existence and genericity, Morse lemma )
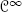All manifolds and functions we consider here are of class Picture 7 , even if, in general, 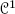Morse Theory and Floer Homology - image 8 regularity suffices!
1.1 Definition of Morse Functions
1.1.a Critical Points, Nondegeneracy
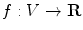Let V be a manifold and let Morse Theory and Floer Homology - image 9 be a function. A critical point of f is a point x such that ( df ) x =0.
Remark 1.1.1
We know that at least if V is compact, f always has critical points, since it has at least a minimum and a maximum.
At a critical point of f we can define the Hessian or second-order derivative.
Remark 1.1.2
Recall that a function on a manifold does not have a second-order derivative: we can always compute a second-order derivative in a chart, but the result depends on the choice of the chart. The second-order derivative is well defined on the kernel of the first-order derivative We will content ourselves with defining it at the critical points. See Exercise 1 on p. 18.
Rather than using a chart and showing that the result does not depend on it, let us invoke a more intrinsic argument (as in [, p. 4]). If x is a critical point of f and if X and Y are vectors tangent to V at x , then we set
where denotes a vector field extending Y locally Since the expression is a - photo 10
where denotes a vector field extending Y locally Since the expression is a - photo 11
Next page
1234567...213
Light

Font size:

↓
↑
Reset

Interval:

↓
↑

Bookmark:

Make

Similar books «Morse Theory and Floer Homology»

Look at similar books to Morse Theory and Floer Homology. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.


Jeswant Gembali - Morse Code made Easy: Concepts
Morse Code made Easy: Concepts
Jeswant Gembali
Morse Code made Easy: Concepts
H. Morse (Henry Morse) Stephens - Revolutionary Europe, 1789-1815
Revolutionary Europe, 1789-1815
H. Morse (Henry Morse) Stephens
Revolutionary Europe, 1789-1815
No cover
No cover
Flo Morse
The Story of the Shakers
J. J. Morse - Practical Occultism
Practical Occultism
J. J. Morse
Practical Occultism
Weyl Hermann - Concept of a Riemann Surface
Concept of a Riemann Surface
Weyl Hermann
Concept of a Riemann Surface
Wagner - Homology, Genes, and Evolutionary Innovation
Homology, Genes, and Evolutionary Innovation
Wagner
Homology, Genes, and Evolutionary Innovation
Edward S. Morse - Japanese Homes and Their Surroundings
Japanese Homes and Their Surroundings
Edward S. Morse
Japanese Homes and Their Surroundings
No cover
No cover
Phil Morse [Morse
Rock The Dancefloor: The proven five-step formula for total DJing success
David Bishop - The Complete Inspector Morse
The Complete Inspector Morse
David Bishop
The Complete Inspector Morse
Jean-Claude Hausmann - Mod Two Homology and Cohomology
Mod Two Homology and Cohomology
Jean-Claude Hausmann
Mod Two Homology and Cohomology
Liviu Nicolaescu - An Invitation to Morse Theory
An Invitation to Morse Theory
Liviu Nicolaescu
An Invitation to Morse Theory
Jackie Morse Kessler - Hunger
Hunger
Jackie Morse Kessler
Hunger
Reviews about «Morse Theory and Floer Homology»

Discussion, reviews of the book Morse Theory and Floer Homology and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.