Jean-Claude Hausmann - Mod Two Homology and Cohomology
Here you can read online Jean-Claude Hausmann - Mod Two Homology and Cohomology full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2014, publisher: Springer, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Mod Two Homology and Cohomology
- Author:
- Publisher:Springer
- Genre:
- Year:2014
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Mod Two Homology and Cohomology: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Mod Two Homology and Cohomology" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Cohomology and homology modulo 2 helps the reader grasp more readily the basics of a major tool in algebraic topology. Compared to a more general approach to (co)homology this refreshing approach has many pedagogical advantages:
1. It leads more quickly to the essentials of the subject,
2. An absence of signs and orientation considerations simplifies the theory,
3. Computations and advanced applications can be presented at an earlier stage,
4. Simple geometrical interpretations of (co)chains.
Mod 2 (co)homology was developed in the first quarter of the twentieth century as an alternative to integral homology, before both became particular cases of (co)homology with arbitrary coefficients.
The first chapters of this book may serve as a basis for a graduate-level introductory course to (co)homology. Simplicial and singular mod 2 (co)homology are introduced, with their products and Steenrod squares, as well as equivariant cohomology. Classical applications include Brouwers fixed point theorem, Poincar duality, Borsuk-Ulam theorem, Hopf invariant, Smith theory, Kervaire invariant, etc. The cohomology of flag manifolds is treated in detail (without spectral sequences), including the relationship between Stiefel-Whitney classes and Schubert calculus. More recent developments are also covered, including topological complexity, face spaces, equivariant Morse theory, conjugation spaces, polygon spaces, amongst others. Each chapter ends with exercises, with some hints and answers at the end of the book.
Jean-Claude Hausmann: author's other books
Who wrote Mod Two Homology and Cohomology? Find out the surname, the name of the author of the book and a list of all author's works by series.
Mod Two Homology and Cohomology — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Mod Two Homology and Cohomology" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
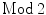homology first occurred in 1908 in a paper of Tietze [196] (see also [40, pp. 4142]). Several results were first established using this 
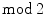approach, like the linking number for submanifolds in 
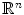(see Sect. ), as well as Alexander duality [7]. One argument in favor of the choice of the 
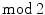homology was its simplicity, as J.W. Alexander says in his introduction: The theory of connectivity [homology] may be approached from two different angles depending on whether or not the notion of sense [orientation] is developed and taken into consideration. We have adopted the second and somewhat simpler point of view in this discussion in order to condense the necessary preliminaries as much as possible. A treatment involving the idea of sense would be somewhat more complicated but would follow along much the same lines.
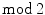homology sometimes gives new theorems. The first historical main example is the generalization of Poincar duality to all closed manifolds, whether orientable or not, a result obtained by Veblen and Alexander in 1913 [200]. As a consequence, the Euler characteristic of a closed odd-dimensional manifold vanishes.
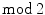cohomology the status of a major tool in algebraic topology, providing for instance the theory of spin structures and Thoms work on the cobordism ring.
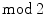(co)homology (there will be essentially no other). They include classical applications (Brouwer fixed point theorem, Poincar duality, Borsuk-Ulam theorem, Smith theory, etc) and less classical ones (face spaces, topological complexity, equivariant Morse theory, etc). The cohomology of flag manifolds is treated in details, including for Grassmannians the relationship between Stiefel-Whitney classes and Schubert calculus. Some original applications are given in Chap..
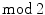(co)homology is just a particular case of (co)homology with arbitrary coefficients. Also, most authors start with a full account of homology before approaching cohomology. In these notes, 
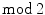(co)homology is treated as a subject by itself and we start with cohomology and homology together from the beginning. The advantages of this approach are the following. - The definition of a (co)chain is simple and intuitive: an (say, simplicial) m-cochain is a set of
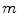-simplexes; an m-chain is a finite set of 
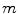-simplexes. The concept of cochain is simpler than that of chain (one less word in the definition 
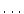), more flexible and somehow more natural. We thus tend to consider cohomology as the main concept and homology as a (useful) tool for some arguments. - Working with
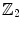and its standard linear algebra is much simpler than working with 
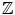. For instance, the Kronecker pairing has an intuitive geometric interpretation occurring at the beginning which shows in an elementary way that cohomology is the dual of homology. Several computations, like the homology of surfaces, are quite easy and come early in the exposition. Also, the cohomology ring is commutative . The cup square 
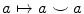is a linear map and may be also non-trivial in odd degrees, leading to important invariants. - The absence of sign and orientation considerations is an enormous technical simplification (even of importance in computer algorithms computing homology). With much lighter computations and technicalities, the ideas of proofs are more apparent.
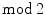(co)homology and taking advantage of its above mentioned simplicity is a great help to grasp the ideas of the subject. The technical difficulties of signs and orientations for finer theories, like integral (co)homology, may then be introduced afterwards, as an adaptation of the more intuitive 
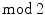(co)homology.- Augmented (co)chain complexes. The reduced cohomology
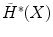is defined as 
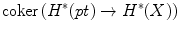for the unique map 
. - Simplicial approximation.
- Spectral sequences (except in the proof of Proposition ).
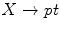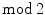cohomology are only briefly surveyed, like the work by Adams on the Hopf-invariant-one problem (p. 353), the Sullivans conjecture (pp. 240 and 353) and the Kervaire invariant (Sect. ).- general point set topology (compactness, connectedness, etc).
- elementary language of categories and functors.
- simple techniques of exact sequences, like the five lemma.
- elementary facts about fundamental groups, coverings and higher homotopy groups (not much used).
- elementary techniques of smooth manifolds.
Font size:
Interval:
Bookmark:
Similar books «Mod Two Homology and Cohomology»
Look at similar books to Mod Two Homology and Cohomology. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Mod Two Homology and Cohomology and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.