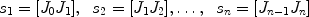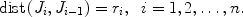Liviu Nicolaescu Universitext An Invitation to Morse Theory 10.1007/978-1-4614-1105-5_1 Springer Science+Business Media, LLC 2012
1. Morse Functions
Liviu Nicolaescu 1
(1)
Department of Mathematics, University of Notre Dame, Notre Dame, USA
Abstract
In this first chapter, we introduce the reader to the main characters of our story, namely, the Morse functions, and we describe the properties which make them so useful. We describe their very special local structure (Morse lemma) and then we show that there are plenty of them around.
In this first chapter, we introduce the reader to the main characters of our story, namely, the Morse functions, and we describe the properties which make them so useful. We describe their very special local structure (Morse lemma) and then we show that there are plenty of them around.
1.1 The Local Structure of Morse Functions
Suppose that F : M N is a smooth (i.e., C ) map between smooth manifolds. The differential of F defines for every x M a linear map
Definition 1.1.
(a)
The point x M is called a critical point of F if
A point x M is called a regular point of F if it is not a critical point. The collection of all critical points of F is called the critical set of F and is denoted by { Cr } F .
(b)
The point y N is called a critical value of F if the fiber F 1( y ) contains a critical point of F . A point y N is called a regular value of F if it is not a critical value. The collection of all the critical values of F is called the discriminant set of F and is denoted by F .
(c)
A subset S N is said to be negligible if for every smooth open embedding
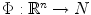
, n =dim N , the preimage 1( S ) has Lebesgue measure zero in
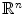
.
Theorem 1.2 (MorseSardFederer).
Suppose that M and N are smooth manifolds and F : M N is a smooth map. Then, the Hausdorff dimension of the discriminant set F is at most dim N 1. In particular, the discriminant set is negligible in N. Moreover, if F(M) has nonempty interior, then the set of regular values is dense in F(M).
For a proof, we refer to Federer [Fed, Theorem 3.4.3] or Milnor [M2].
Remark 1.3.
(a)
If M and N are real analytic manifolds and F is a proper real analytic map, then we can be more precise. The discriminant set is a locally finite union of real analytic submanifolds of N of dimensions less than dim N . Exercise 6.1 may perhaps explain why the set of critical values is called discriminant.
(b)
The range of a smooth map F : M N may have empty interior. For example, the range of the map
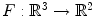
, F ( x , y , z )=( x ,0), is the x -axis of the Cartesian plane
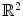
. The discriminant set of this map coincides with the range.
Example 1.4.
Suppose
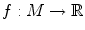
is a smooth function. Then, x 0 M is a critical point of f if and only if
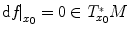
.
Suppose M is embedded in an Euclidean space E and
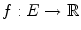
is a smooth function. Denote by f M the restriction of f to M . A point x 0 M is a critical point of f M if
This happens if either x 0 is a critical point of f , or
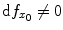
and the tangent space to M at x 0 is contained in the tangent space at x 0 of the level set { f = f ( x 0)}. If f happens to be a nonzero linear function, then all its level sets are hyperplanes perpendicular to a fixed vector
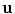
, and x 0 M is a critical point of f M if and only if
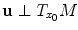
, i.e., the hyperplane determined by f and passing through x 0 is tangent to M .
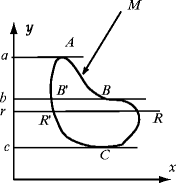
In Fig., we have depicted a smooth curve
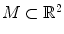
. The points A , B ,and C are critical points of the linear function f ( x , y )= y . The level sets of this function are horizontal lines and the critical points of its restriction to M are the points where the tangent space to the curve is horizontal. The points a , b ,and c on the vertical axis are critical values, while r is a regular value.
Example 1.5 ( Robot arms: critical configurations ).
We begin in this example the study of the critical points of a smooth function which arises in the design of robot arms. We will discuss only a special case of the problem when the motion of the arm is constrained to a plane. For slightly different presentations, we refer to the papers [Hau, KM, SV], which served as our sources of inspiration. The paper [Hau] discusses the most general version of this problem, when the motion of the arm is not necessarily constrained to a plane.
Fig. 1.1
The height function on a smooth curve in the plane
Fix positive real numbers r 1, , r n>0, n 2. A (planar) robot arm (or linkage) with n segments is a continuous curve in the Euclidean plane consisting of n line segments
of lengths
We will refer to the vertices J i as the joints of the robot arm. We assume that J 0 is fixed at the origin of the plane, and all the segments of the arm are allowed to rotate about the joints. Additionally, we require that the last joint be constrained to slide along the positive real semiaxis (see Fig.).
Fig. 1.2
A robot arm with four segments
A (robot arm) configuration is a possible position of the robot arm subject to the above constraints. Mathematically a configuration is described by an n -uple













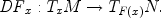
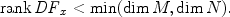
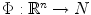 , n =dim N , the preimage 1( S ) has Lebesgue measure zero in
, n =dim N , the preimage 1( S ) has Lebesgue measure zero in 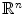 .
.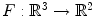 , F ( x , y , z )=( x ,0), is the x -axis of the Cartesian plane
, F ( x , y , z )=( x ,0), is the x -axis of the Cartesian plane 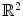 . The discriminant set of this map coincides with the range.
. The discriminant set of this map coincides with the range.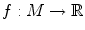 is a smooth function. Then, x 0 M is a critical point of f if and only if
is a smooth function. Then, x 0 M is a critical point of f if and only if 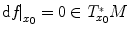 .
.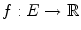 is a smooth function. Denote by f M the restriction of f to M . A point x 0 M is a critical point of f M if
is a smooth function. Denote by f M the restriction of f to M . A point x 0 M is a critical point of f M if 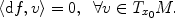
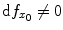 and the tangent space to M at x 0 is contained in the tangent space at x 0 of the level set { f = f ( x 0)}. If f happens to be a nonzero linear function, then all its level sets are hyperplanes perpendicular to a fixed vector
and the tangent space to M at x 0 is contained in the tangent space at x 0 of the level set { f = f ( x 0)}. If f happens to be a nonzero linear function, then all its level sets are hyperplanes perpendicular to a fixed vector 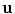 , and x 0 M is a critical point of f M if and only if
, and x 0 M is a critical point of f M if and only if 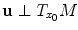 , i.e., the hyperplane determined by f and passing through x 0 is tangent to M .
, i.e., the hyperplane determined by f and passing through x 0 is tangent to M .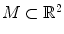 . The points A , B ,and C are critical points of the linear function f ( x , y )= y . The level sets of this function are horizontal lines and the critical points of its restriction to M are the points where the tangent space to the curve is horizontal. The points a , b ,and c on the vertical axis are critical values, while r is a regular value.
. The points A , B ,and C are critical points of the linear function f ( x , y )= y . The level sets of this function are horizontal lines and the critical points of its restriction to M are the points where the tangent space to the curve is horizontal. The points a , b ,and c on the vertical axis are critical values, while r is a regular value.