Chamberland - Single digits : in praise of small numbers

single digits

single digits

In Praise of Small Numbers

MARC CHAMBERLAND

Princeton University Press

Princeton & Oxford

Copyright 2015 by Princeton University Press

Published by Princeton University Press, 41 William Street, Princeton,
New Jersey 08540

In the United Kingdom: Princeton University Press, 6 Oxford Street,
Woodstock, Oxfordshire OX20 1TW
press.princeton.edu

All Rights Reserved

The second epigraph by Paul McCartney on page 111 is taken from The Beatles and is reproduced with permission of Curtis Brown Group Ltd.,
London on behalf of The Beneficiaries of the Estate of Hunter Davies.

Copyright Hunter Davies 2009.

The epigraph on page 170 is taken from Harry Potter and the Half Blood Prince: Copyright J.K. Rowling 2005

The epigraphs on page 205 are reprinted wiht the permission of the Free Press, a Division of Simon & Schuster, Inc., from Born on a Blue Day: Inside the Extraordinary Mind of an Austistic Savant by Daniel Tammet.

Copyright 2006 by Daniel Tammet. Originally published in Great Britain in 2006 by Hodder & Stoughton. All rights reserved.

Library of Congress Cataloging-in-Publication Data

Chamberland, Marc, 1964
Single digits : in praise of small numbers / Marc Chamberland.
pages cm

Includes bibliographical references and index.

ISBN 978-0-691-16114-3 (hardcover : alk. paper) 1. Mathematical analysis. 2. Sequences (Mathematics) 3. Combinatorial analysis. 4. MathematicsMiscellanea. I. Title.

QA300.C4412 2015

510dc23 2014047680

British Library Cataloging-in-Publication Data is available

This book has been composed in Adobe Caslon Pro and Myriad Pro

Printed on acid-free paper.

Typeset by S R Nova Pvt Ltd, Bangalore, India

Printed in the United States of America

1 3 5 7 9 10 8 6 4 2

contents

preface

When you have mastered numbers, you will in fact no longer be reading numbers, any more than you read words when reading books. You will be reading meanings.

W. E. B. Du Bois

A colorful story concerns two mathematical wizards of early twentieth-century Britain, G. H. Hardy, the intellectually towering professor from Cambridge, and Srinivasa Ramanujan, the young genius from India. Their unlikely collaboration culminated in Hardys invitation to bring Ramanujan to England to jointly pursue research. After a few years, Ramanujan fell illdiagnosed with tuberculosisand was confined to a sanatorium. Hardy recounts an unusual conversation during a visit to Ramanujan:

I remember once going to see him when he was ill at Putney. I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavorable omen. No, he replied, it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways (Hardy, Ramanujan, p. 12).

Indeed, one can write 1729 = 13 + 123 = 93 + 103. How does one come up with such observations? You have to study the numbers for a long time and make many connections. With talent, burning curiosity, and few distractions, Ramanujan became the master of numbers. J. E. Littlewood, Hardys longtime collaborator, commented upon hearing the taxicab story, Every positive integer is one of Ramanujans personal friends.

This book is about single digits, specifically, the numbers 1 to 9. While it was tempting to also include the number zero, I decided to stick with the counting numbers. Each number has fascinating properties connected to many different areas of mathematics, including number theory, geometry, chaos, numerical analysis, mathematical physics, and much more. Some of the topics, such as the Pizza Theorem, require little mathematical background and are understandable by a curious 12-year-old; other sections require modest amounts of technical math, while a few sections, such as the section on E8, allude to such sufficiently advanced material that it should not be read with small children present. Virtually every section is an independent vignette. For the cautious reader, the easier sections tend to lead off each chapter, and the earlier chapters are easier as a whole. Some of these topics are further explored in my YouTube channel, Tipping Point Math. There is assuredly something new and enlightening for everyone, the numbers 1 to 9 connecting to a multitude of mathematics in magical ways. I hope that you will come to call these numbers your friends.

I am grateful to my Grinnell colleagues Chris French, Joe Mileti, and Jen Paulhus and other mathematical colleagues Art Benjamin and Mike Mossinghoff for helpful advice. Its wonderful to have a network of bright, resourceful people who can offer thoughtful, timely answers when needed. Special thanks go to my editor Vickie Kearn at Princeton University Press for her support all along the way. Lastly, I want to thank my family, especially my wife Marion, for encouragement during the long writing process. All this help leaves me positively disposed for future projects.

single digits

The Number One

All for one and one for all.

The Three Musketeers by Alexandre Dumas

Even if you are a minority of one, the truth is the truth.

Mahatma Gandhi

The number one seems like such an innocuous value. What can you do with only one thing? But the simplicity of one can be couched in a positive light: uniqueness. We all know that being single has its virtues. In a mathematical world with so many apparent options, having exactly one possibility is a valued commodity. A search of mathematical research papers and books found that more than 2,700 had the word unique in their titles. Knowing that there is a unique solution to a problem can imply structure and strategies for solving. Some (but not all) of the sections in this chapter explore how uniqueness arises in diverse mathematical contexts. This brings new meaning to looking for the one.

Sliced Origami

Origami traditionally requires that one start with a square piece of paper and attain the final form by only folding. When mathematicians seriously entered the world of origami, they began to systematize constructions, including the use of computers to make precise fold patterns. Besides adding to the art, their contributions have also led to practical applications. For example, how can one transport a solar panel array into space? Mathematical origami has produced a design that compactly stores the whole assembly for transport. Once in space, the array is unfolded to its full size.

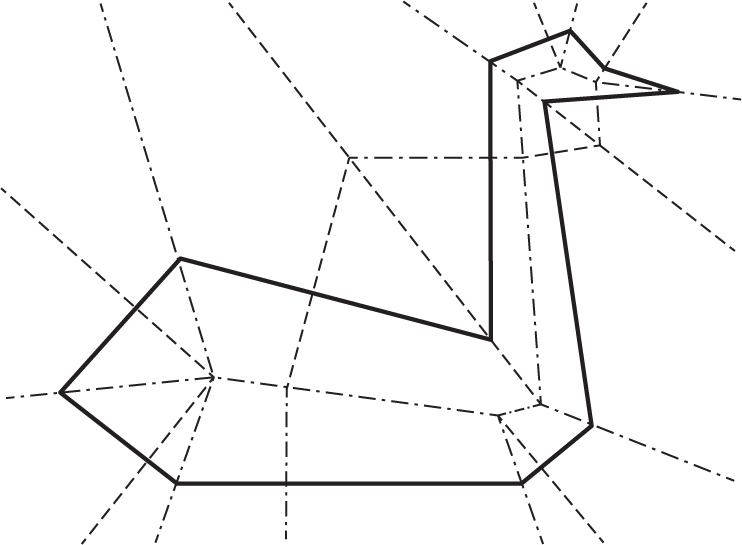
F IGURE 1.1: Origami fold pattern for a swan.

Children have long made beautiful paper snowflakes, but such constructions violate a fundamental origami tradition: no cutting, tearing, or gluing. But what if we were allowed a single cut? What new patterns could be attained? The surprising answer was found by Erik Demaine, a young Canadian professor at MIT, whose research intersects art, mathematics, and computer science. Demaine proved that any pattern whose boundary involves a finite number of straight line segments can be made by folding a paper appropriately and making a single cut! The possibilities include any polygon or multiple polygons. demonstrates the fold pattern needed to make a swan. After folding along each of the dashed and dashed-dot lines, the figure can be collapsedwith practiceso that a single cut along the bold line produces the swan.

Fibonacci Numbers and the Golden Ratio