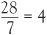mathematical ideas
you really need to know

Tony Crilly
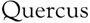
Contents
Introduction
Mathematics is a vast subject and no one can possibly know it all. What one can do is explore and find an individual pathway. The possibilities open to us here will lead to other times and different cultures and to ideas that have intrigued mathematicians for centuries.
Mathematics is both ancient and modern and is built up from widespread cultural and political influences. From India and Arabia we derive our modern numbering system but it is one tempered with historical barnacles. The base 60 of the Babylonians of two or three millennia BC shows up in our own culture we have 60 seconds in a minute and 60 minutes in an hour; a right angle is still 90 degrees and not 100 grads as revolutionary France adopted in a first move towards decimalization.
The technological triumphs of the modern age depend on mathematics and surely there is no longer any pride left in announcing to have been no good at it when at school. Of course school mathematics is a different thing, often taught with an eye to examinations. The time pressure of school does not help either, for mathematics is a subject where there is no merit in being fast. People need time to allow the ideas to sink in. Some of the greatest mathematicians have been painfully slow as they strove to understand the deep concepts of their subject.
There is no hurry with this book. It can be dipped into at leisure. Take your time and discover what these ideas you may have heard of really mean. Beginning with Zero, or elsewhere if you wish, you can move on a trip between islands of mathematical ideas. For instance, you can become knowledgeable about Game theory and next read about Magic squares. Alternatively you can move from Golden rectangles to the famous Fermats last theorem, or any other path.
This is an exciting time for mathematics. Some of its major problems have been solved in recent times. Modern computing developments have helped with some but been helpless against others. The Four-colour problem was solved with the aid of a computer, but the Riemann hypothesis, the final chapter of the book, remains unsolved by computer or any other means.
Mathematics is for all. The popularity of Sudoku is evidence that people can do mathematics (without knowing it) and enjoy it too. In mathematics, like art or music, there have been the geniuses but theirs is not the whole story. You will see several leaders making entrances and exits in some chapters only to reappear in others. Leonhard Euler, whose tercentenary occurs in 2007, is a frequent visitor to these pages. But, real progress in mathematics is the work of the many accumulated over centuries. The choice of 50 topics is a personal one but I have tried to keep a balance. There are everyday and advanced items, pure and applied mathematics, abstract and concrete, the old and the new. Mathematics though is one united subject and the difficulty in writing has not been in choosing topics, but in leaving some out. There could have been 500 ideas but 50 are enough for a good beginning to your mathematical career.
Zero
At a young age we make an unsteady entrance into numberland. We learn that 1 is first in the number alphabet, and that it introduces the counting numbers 1, 2, 3, 4, 5,... Counting numbers are just that: they count real things apples, oranges, bananas, pears. It is only later that we can count the number of apples in a box when there are none.
Even the early Greeks, who advanced science and mathematics by quantum leaps, and the Romans, renowned for their feats of engineering, lacked an effective way of dealing with the number of apples in an empty box. They failed to give nothing a name. The Romans had their ways of combining I, V, X, L, C, D and M but where was 0? They did not count nothing.
How did zero become accepted?
The use of a symbol designating nothingness is thought to have originated thousands of years ago. The Maya civilization in what is now Mexico used zero in various forms. A little later, the astronomer Claudius Ptolemy, influenced by the Babylonians, used a symbol akin to our modern 0 as a placeholder in his number system. As a placeholder, zero could be used to distinguish between examples (in modern notation) such as 75 and 705, instead of relying on context as the Babylonians had done. This might be compared with the introduction of the comma into language both help with reading the right meaning. But, just as the comma comes with a set of rules for its use there have to be rules for using zero.
The seventh-century Indian mathematician Brahmagupta treated zero as a number, not merely as a placeholder, and set out rules for dealing with it. These included the sum of a positive number and zero is positive and the sum of zero and zero is zero. In thinking of zero as a number rather than a placeholder, he was quite advanced. The Hindu-Arabic numbering system which included zero in this way was promulgated in the West by Leonardo of Pisa Fibonacci in his Liber Abaci ( The Book of Counting ) first published in 1202. Brought up in North Africa and schooled in the Hindu-Arabian arithmetic, he recognized the power of using the extra sign 0 combined with the Hindu symbols 1, 2, 3, 4, 5, 6, 7, 8 and 9.
The launch of zero into the number system posed a problem which Brahmagupta had briefly addressed: how was this interloper to be treated? He had made a start but his nostrums were vague. How could zero be integrated into the existing system of arithmetic in a more precise way? Some adjustments were straightforward. When it came to addition and multiplication, 0 fitted in neatly, but the operations of subtraction and division did not sit easily with the foreigner. Meanings were needed to ensure that 0 harmonized with the rest of accepted arithmetic.
How does zero work?
Adding and multiplying with zero is straightforward and uncontentious you can add 0 to 10 to get a hundred but we shall amean add in the less imaginative way of the numerical operation. Adding 0 to a number leaves that number unchanged while multiplying 0 by any number always gives 0 as the answer. For example, we have 7 + 0 = 7 and 7 0 = 0. Subtraction is a simple operation but can lead to negatives, 7 0 = 7 and 0 7 = 7, while division involving zero raises difficulties.
Lets imagine a length to be measured with a measuring rod. Suppose the measuring rod is actually 7 units in length. We are interested in how many measuring rods we can lie along our given length. If the length to be measured is actually 28 units the answer is 28 divided by 7 or in symbols 2 8 7 = 4. A better notation to express this division is
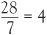
and then we can cross-multiply to write this in terms of multiplication, as 2 8 = 7 4. What now can be made of 0 divided by 7? To help suggest an answer in this case let us call the answer a so that
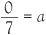
By cross-multiplication this is equivalent to 0 = 7 a . If this is the case, the only possible value for a is 0 itself because if the multiplication of two numbers gives 0, one of them must be 0. Clearly it is not 7 so a must be a zero.
This is not the main difficulty with zero. The danger point is division