Table of Contents
the universe cannot be understood unless one first learns to comprehend the language and interpret the characters in which it is written. It is written in the language of mathematics, and its characters are geometric figures without which it is humanly impossible to understand a single word of it; without these, one is wandering in a dark labyrinth.
Galileo Galilei
Other books by Theoni Pappas
The Joy of Mathematics
More Joy of Mathematics
The Mathematics Calendar
Magic of Mathematics
Mathematical Scandals
The Music of Reason
Mathematics Appreciation
Math Talk
Greek Cooking For Everyone
Math-A-Day
Math Stuff
Mathematical Snippets
Other childrens books by Theoni Pappas
Fractals, Googols & Other Mathematical Tales
The Childrens Mathematics Calendar
Math for Kids & Other People Too!
Adventures of PenroseThe Mathematics Cat
Math Talk
To Elvira
for her constant
encouragement and support
&
contagious enthusiasm
With me everything turns into mathematics.
Ren Descartes
introduction
As we look around us, occasionally we see subtle impressions of the presence of mathematics. Some are current, some are left from past centuries. Tracking and discovering the trail of mathematical footprints is both fascinating and rewarding. These impressions help us understand our world and the universe, even as we discover the enormous influence of mathematics on our lives.
The first mathematical footprints date back to prehistoric times. Left on the walls of prehstoric caves are marks or symbols meant to keep track of things perhaps the passage of time, the quantity of things gathered or bartered.
Over thousands of years, mathematics has revealed its influence in art, mysticism of numbers, commerce and trade, architecture, the sciences, Mathematics is so subtle, pervasive, and necessary in our daily lives, we often are oblivious to its presence. Yet, with each passing day, mathematics is expanding its realm, placing its mark in more and more areas. Today, science could not function without mathematical tools, nor could we bank, build, travel, be entertained, enter the realm of electronics, invent, or explore the universe.
Mathematical Footprints follows the trail of mathematics. The order in which these mathematical footprints is presented is random, simply because that is often how they occur. For example, the Pythagoreans did not expect to uncover irrational numbers in the diagonal of a square. Nor did Fibonacci or future mathematicians expect the Fibonacci numbers to be so prevalent in nature. Or, who would have predicted fractals would become so important in describing everyday objects? History illustrates over and over that mathematical ideas have a connection to the physical world, and usually when we least expect it.
I invite you to open this book at random, and discover a mathematical footprint. Perhaps you will be left wondering, as I am, whether the first mathematical idea was born in a prehistoric cave or whether mathematical ideas are timeless universal truths waiting to be uncovered.
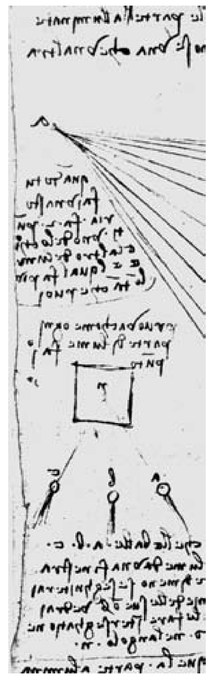
Work on perspective as it appears in a portion of a page from one of Leonardo da Vincis manuscripts.
the ingenious method of expressing all numbers by means of ten symbols, each symbol receiving a value of position as well as an absolute value appears so simple to us now that we ignore its true merits. But its very simplicityputs our arithmetic in the first rank of useful inventions
Pierre-Simon Laplace
early mathematics artifacts
Holding a dim light up to etched marks on the walls of caves in La Pileta, Spain, one is struck by the realization that some of these prehistoric markings are not petroglyph art or figures. Rather, they resemble something innately familiarcounting marks of some sort. What were these cave dwellers tallying? Are these examples of prehistoric mathematics? Only our imagination and intuition can supply possible answers. The earliest counting artifacts available from prehistoric times appeared in cave drawings. But that did not preclude the use of piles of stones, marks made in the dust, or marks etched in bones, in stones and on sticks. Five marks grouped together is a recurring theme found on notched bones. These early people were familiar with the five digits of their hands, so it is not surprising to find evidence of tallying by fives.
Tally marks from the Pileta cave
cone and sphere impressions on clay
The evolution of numbers in the Sumerian civilization gives a glimpse of how abstract numbers may have evolved. The Sumerians first used clay tokens to represent commodities. Grain, for example was represented by a cone or sphere, while a cylinder shape represented an animal. As commodities shifted from agriculturally related things to merchandise, new more complicated tokens clay envelopes (clay spherical containers). These envelopes could be used as receipts or even contracts. The merchandise tokens were strung on a clay band, perhaps so they could be easily reviewed. If one lost track of what was concealed in a clay envelop, the only way to find out its contents was to break it open, thereby breaking a possible agreement. Eventually, circle indentations(for the sphere) and pointed indentations (for the cone) were marked on the outside of the clay envelop to indicate its contents. Thus, the concept for a symbol gradually evolved. For example, three trees and two units of grain were first represented by three cones and two sphere tokens. These tokens were then represented by impressions on the outside of the envelopthree impressed pointed symbols for three cones and two circles for two spheres. The same recording process was eventually developed for the other tokens. As the societys function became more complicated, new recording methods evolved. From here the Sumerians went on to use a wedge shape to stand for 1 and a circle for 10. So, 15 was written
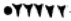
. To these a larger wedge was invented to represent 60 and a larger circle for 360. Their early number system had aspects of both base ten and base sixty, yet it was not a positional system until around 2400 BC. This method of notation spread throughout the Middle East.
How seven urns were depicted on the Pylos tablets from Crete.

Ancient mathematical artifacts appear all over the world. In England we find Stonehenge(2000BC), possibly a primitive computer for predicting lunar and solar events. On the island of Crete, clay tablets were unearthed with Linear B inscriptions listing such things as farm animals, bathtubs, bronze and gold. The early Hindu numerals in the 3rd century BC had inscriptions of King Asoka (2nd century BC) which were found in a cave in Nn Ght. Numerals from the 1st and 2nd centuries were found in the Nasik caves of India. The discovery of the Rhind and Golonishev papyrus revealed mathematical work from ancient Egypt. These papyruses contained a wealth of problems which used both whole numbers and fractions in their solutions. Among these are problems dealing with basic operations, linear equations, tables, practical geometric problems involving circles, rectangles, triangles and pyramids, and measurements and inventories. In a guard post along the Great Wall of China a pile of wooden sticks was uncovered, which have come to be called the Han Sticks. These sticks are from the time of the Han Dynasty (ca.200BC to 200AD) and record daily activities of the Chinese living around that portion of the Great Wall. These simple wooden sticks, among other things, reveal information about troops, their duties, payments for bricks used to build the wall, and distances of operations. The numerals appearing on these sticks show tallies written from the top down, the same direction used in China today. Instead of the traditional way, they also reveal a shortcut-like method for writing the numerals for 20, 30, and 40. These artifacts show that as the functions of a civilization become more complicated, more sophisticated mathematics is needed to handle its many tasks. Yet, artifacts need be kept in perspective, for they only furnish a peek into the past. Imagine if someones income tax return was used as a mathematical artifact for our period. What would they surmise about our mathematics?















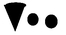
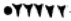 . To these a larger wedge was invented to represent 60 and a larger circle for 360. Their early number system had aspects of both base ten and base sixty, yet it was not a positional system until around 2400 BC. This method of notation spread throughout the Middle East.
. To these a larger wedge was invented to represent 60 and a larger circle for 360. Their early number system had aspects of both base ten and base sixty, yet it was not a positional system until around 2400 BC. This method of notation spread throughout the Middle East.