Table of Contents
I hope this book will serve as an introduction to some of the many diversified facets of mathematics, and that the reader will be encouraged to explore in greater depth the ideas presented.
Theoni Pappas
the universe stands continually open to our gaze, but it cannot be understood unless one first learns to comprehend the language and interpret the characters in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures, without which it is humanly impossible to understand a single word of it; without these, one is wandering about in a dark labyrinth.
Galileo
INTRODUCTION
The Joy Of Mathematics and More Joy of Mathematics unveil concepts, ideas, questions, history, problems, and pastimes which reveal the influence and nature of mathematics.
To experience the joy of mathematics is to realize mathematics is not some isolated subject that has little relationship to the things around us other than to frustrate us with unbalanced check books and complicated computations. Few grasp the true nature of mathematicsso entwined in our environment and in our lives. So many things around us can be described by mathematics. Mathematical concepts are even inherent in the structure of living cells.
These books seek to help you become aware of the inseparable relationship of mathematics and the world by presenting glimpses and images of mathematics in the many facets of our lives.
The joy of mathematics is similar to the experience of discovering something for the first time. It is an almost child-like feeling of wonder. Once you have experienced it you will not forget that feelingit can be as exciting as looking into a microscope for the first time and seeing things that have always been around you that you have been unable to see before.
When deciding how to organize The Joy Of Mathematics, at first certain divisions immediately came to mindfor example, mathematics and nature, mathematics and science, mathematics and art, and so forth. But mathematics and its relationship to our surroundings does not come already packaged into categories. Rather, mathematics and its occurrences are spontaneous with elements of surprise. Thus, the topics are randomly arranged to retain the true essence of discovery. The Joy Of Mathematics and More Joy of Mathematics are designed to be opened at any point. Each section, regardless of how large or small, is essentially self-contained.
After one experiences the sheer joy of mathematics, the appreciation of mathematics follows and then the desire to learn more.
There is no branch of mathematics, however abstract, which may not someday be applied to the phenomena of the real world.
Lobachevsky
Mathematics is a science, a language, an art, a way of thinking. Appearing in nature, art, music, architecture, history, science literatureits influence is present in every facet of the universe. Mathematics is a figment of the imagination. All its elements, objects, axioms, theorems, definitions describe objects which do not actually exist in our world. The worlds created by mathematicians are imaginary. They exist independently of anything in our world. Mathematics can be used to describe, explain and predict phenomena of the universe; but mathematical objects were not necessarily created with that purpose in mind. What stimulates the mathematicians imagination?an interesting pattern, an intriguing problem, a theorem or postulate, a challenge to determine a solution, an unanswered question, or simply curiosity and determination to discover a truth.
Theoni Pappas
The Evolution of BaseTen
Early forms of counting had no positional base value system. But around 1700 B.C. the positional base 60 evolved. It was very helpful to the Mesopotamians who developed it to use in conjunction with their 360 day calendar. The oldest known true place value system is that devised by the Babylonians, and was derived from the Sumerian sexigesimal system. Instead of needing sixty symbols to write the numerals from 0 to 59, two symbols

for 1 and
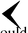
for 10 sufficed. Sophisticated mathematical computations could be performed with it, it, but no symbol for zero had been devised. To indicate zero an empty position was left in the number. About 300 B.C. a symbol for zero appeared,
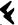
or
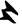
, and the base 60 system developed extensively. In the early A.D. years, the Greeks and Hindus began to use base 10 systems, but they did not have positional notation. They used the first ten letters of their alphabet for counting. Then around 500 A.D. a Hindu invented a positional notation for the base 10 system. He abandoned the letters which had been used for numerals past 9, and standardized the first nine symbols. About 825 A.D., the Arab mathematician
Al-Khowavizmi wrote an enthusiastic book about the Hindu numerals. The base 10 system reached Spain around the 11th century when the Ghobar numerals were formed. Europe was skeptical and slow to change. Scholars and scientists were reticent to employ the base 10 system because it had no simple way to denote fractions. But it became popular when merchants adopted it, since it proved so invaluable in their work and record keeping. Later, decimal fractions made their appearance in the 16th century, and the decimal point was introduced in 1617 by John Napier.

Someday, as our needs and ways of computing change, will a new system evolve and replace base ten?
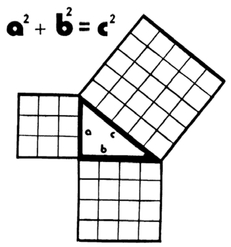
The Pythagorean Theorem
Anyone who has studied algebra or geometry has heard of the Pythagorean Theorem. This famous theorem is used in many branches of mathematics and in construction, architecture and measurement. In ancient times, the Egyptians used their knowledge of this theorem to construct right angles. They knotted ropes with units of 3, 4 and 5 knot spaces. Then, using the three ropes, they stretched them and formed a triangle. They knew the triangle would always end up having a right angle opposite the longest side (32+42=52).
Pythagorean theorem:Given a right triangle, then the square of the hypotenuse of a right triangle equals the sum of the squares of the two legs of the right triangle.
Its converse is also true. If the sum of the squares of two sides of a triangle equals the square of the third side, then the triangle is a right triangle.
Although this theorem is named after the Greek mathematician, Pythagoras (circa 540 B.C.), evidence of the theorem goes back to the Babylonians of Hammurabis time, over 1000 years before Pythagoras. Perhaps the name is attributed to Pythagoras because the first record of written proofs come from his school. The existence of the











 for 1 and
for 1 and 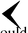 for 10 sufficed. Sophisticated mathematical computations could be performed with it, it, but no symbol for zero had been devised. To indicate zero an empty position was left in the number. About 300 B.C. a symbol for zero appeared,
for 10 sufficed. Sophisticated mathematical computations could be performed with it, it, but no symbol for zero had been devised. To indicate zero an empty position was left in the number. About 300 B.C. a symbol for zero appeared, 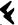 or
or 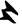 , and the base 60 system developed extensively. In the early A.D. years, the Greeks and Hindus began to use base 10 systems, but they did not have positional notation. They used the first ten letters of their alphabet for counting. Then around 500 A.D. a Hindu invented a positional notation for the base 10 system. He abandoned the letters which had been used for numerals past 9, and standardized the first nine symbols. About 825 A.D., the Arab mathematician Al-Khowavizmi wrote an enthusiastic book about the Hindu numerals. The base 10 system reached Spain around the 11th century when the Ghobar numerals were formed. Europe was skeptical and slow to change. Scholars and scientists were reticent to employ the base 10 system because it had no simple way to denote fractions. But it became popular when merchants adopted it, since it proved so invaluable in their work and record keeping. Later, decimal fractions made their appearance in the 16th century, and the decimal point was introduced in 1617 by John Napier.
, and the base 60 system developed extensively. In the early A.D. years, the Greeks and Hindus began to use base 10 systems, but they did not have positional notation. They used the first ten letters of their alphabet for counting. Then around 500 A.D. a Hindu invented a positional notation for the base 10 system. He abandoned the letters which had been used for numerals past 9, and standardized the first nine symbols. About 825 A.D., the Arab mathematician Al-Khowavizmi wrote an enthusiastic book about the Hindu numerals. The base 10 system reached Spain around the 11th century when the Ghobar numerals were formed. Europe was skeptical and slow to change. Scholars and scientists were reticent to employ the base 10 system because it had no simple way to denote fractions. But it became popular when merchants adopted it, since it proved so invaluable in their work and record keeping. Later, decimal fractions made their appearance in the 16th century, and the decimal point was introduced in 1617 by John Napier.