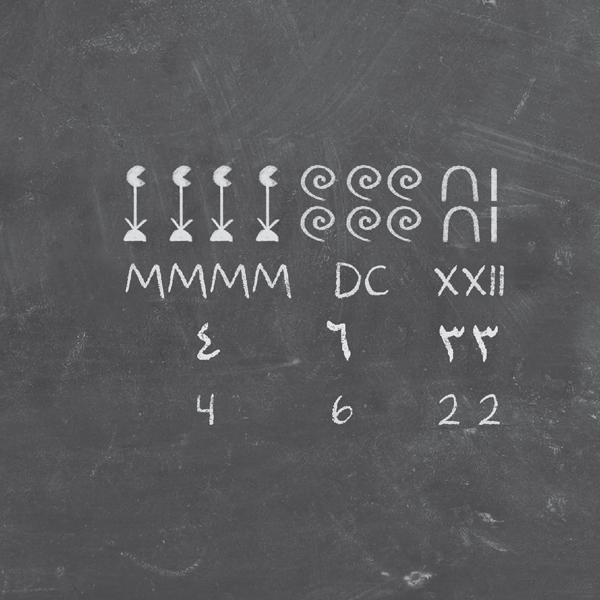Paul Glendinning - Math in minutes: 200 key concepts explained in an instant

Math in Minutes

Math in Minutes

Paul Glendinning

New York London

2012 by Paul Glendinning

First published in the United States by Quercus in 2013

All rights reserved. No part of this book may be reproduced in any form or by any electronic or mechanical means, including information storage and retrieval systems, without permission in writing from the publisher, except by reviewers, who may quote brief passages in a review. Scanning, uploading, and electronic distribution of this book or the facilitation of the same without the permission of the publisher is prohibited.

Please purchase only authorized electronic editions, and do not participate in or encourage electronic piracy of copyrighted materials. Your support of the authors rights is appreciated.

Any member of educational institutions wishing to photocopy part or all of the work for classroom use or anthology should send inquiries to Permissions c/o Quercus Publishing Inc., 31 West 57 th Street, 6 th Floor, New York, NY 10019, or to permissions@quercus.com.

e-ISBN: 978-1-62365-009-4

Distributed in the United States and Canada by Random House Publisher Services

c/o Random House, 1745 Broadway

New York, NY 10019

www.quercus.com

Picture credits:

All pictures are believed to be in the public domain except:

: Sam Daoud/Wikimedia.

Contents

Introduction

M athematics has been evolving for over four thousand years. We still measure angles using the 360-degree system introduced by the Babylonians. Geometry came of age with the ancient Greeks, who also understood irrational numbers. The Moorish civilization developed algebra and popularized the idea of zero as a number.

Mathematics has a rich history for good reason. It is both stunningly usefulthe language of science, technology, architecture, and commerceand profoundly satisfying as an intellectual pursuit. Not only does mathematics have a rich past, but it continues to evolve, both in the sophistication of approaches to established areas and in the discovery or invention of new areas of investigation. Recently computers have provided a new way to explore the unknown, and even if traditional mathematical proofs are the end product, numerical simulations can provide a source of new intuition that speeds up the process of framing conjectures.

Only a lunatic would pretend that all mathematics could be presented in 200 bite-sized chunks. What this book does attempt to do is to describe some of the achievements of mathematics, both ancient and modern, and explain why these are so exciting. In order to develop some of the ideas in more detail it seemed natural to focus on core mathematics. The many applications of these ideas are mentioned only in passing.

The ideas of mathematics build on each other, and the topics in this book are organized so that cognate areas are reasonably close together. But look out for long-range connections. One of the amazing features of mathematics is that apparently separate areas of study turn out to be deeply connected. Monstrous moonshine (page 300) provides a modern example of this, and matrix equations (page 272) a more established link.

This book is thus a heady distillation of four thousand years of human endeavor, but it can only be a beginning. I hope it will provide a springboard for further reading and deeper thought.

Paul Glendinning,

October 2011

Numbers

N umbers at their most elementary are just adjectives describing quantity. We might say, for instance, three chairs or two sheep. But even as an adjective, we understand instinctively that the phrase two and a half goats makes no sense. Numbers, then, can have different uses and meanings.

As ancient peoples used them in different ways, numbers acquired symbolic meanings, like the water lily that depicts the number 1000 in Egyptian hieroglyphs. Although aesthetically pleasing, this visual approach does not lend itself to algebraic manipulation. As numbers became more widely used, their symbols became simpler. The Romans used a small range of basic signs to represent a huge range of numbers. However, calculations using large numbers were still complicated.

Our modern system of numerals is inherited from the Arabic civilizations of the first millennium AD. Using 10 as its base (see ), it makes complex manipulations far easier to manage.

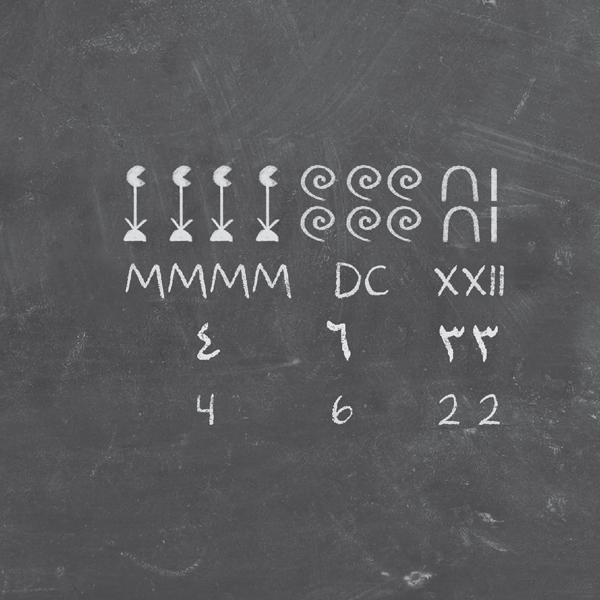
Natural numbers

N atural numbers are the simple counting numbers (0, 1, 2, 3, 4,...). The skill of counting is intimately linked to the development of complex societies through trade, technology, and documentation. Counting requires more than numbers, though. It involves addition, and hence subtraction too.

As soon as counting is introduced, operations on numbers also become part of the lexiconnumbers stop being simple descriptors, and become objects that can transform each other. Once addition is understood, multiplication follows as a way of looking at sums of sumshow many objects are in five groups of six?while division offers a way of describing the opposite operation to multiplicationif thirty objects are divided into five equal groups, how many objects are in each?

But there are problems. What does it mean to divide 31 into 5 equal groups? What is 1 take away 10? To make sense of these questions we need to go beyond the natural numbers.

One

T ogether with zero, the number one is at the heart of all arithmetic. One is the adjective for a single object: by repeatedly adding or subtracting the number to or from itself, all the positive and negative whole numbers, the integers , can be created. This was the basis of tallying, perhaps the earliest system of counting, whose origins can be traced back to prehistoric times. One also has a special role in multiplication: multiplying any given number by one simply produces the original number. This property is expressed by calling it the multiplicative identity .

The number one has unique properties that mean it behaves in unusual waysit is a factor of all other whole numbers, the first nonzero number and the first odd number. It also provides a useful standard of comparison for measurements, so many calculations in mathematics and science are normalized to give answers between zero and one.

Zero

Z ero is a complex idea, and for a long time there was considerable philosophical reluctance to recognize and put a name to it. The earliest zero symbols are only found between other numerals, indicating an absence. The ancient Babylonian number system, for instance, used a placeholder for zero when it fell between other numerals, but not at the end of a number. The earliest definitive use of zero as a number like any other comes from Indian mathematicians around the ninth century.