Paul R. Halmos - Naive Set Theory

Bibliographical Note

This Dover edition, first published in 2017, is an unabridged republication of the work originally published in 1960 by the D. Van Nostrand Company, Inc., Princeton, N.J., as part of The University Series in Undergraduate Mathematics.

Library of Congress Cataloging-in-Publication Data

Names: Halmos, Paul R. (Paul Richard), 1916-2006.

Title: Naive set theory / Paul R. Halmos.

Description: Dover edition. | Mineola, New York : Dover Publications, Inc., 2017. | Originally published: New York : D. Van Nostrand Company, Inc., 1960. | Includes bibliographical references and index.

Identifiers: LCCN 2016043254| ISBN 9780486814872 | ISBN 0486814874

Subjects: LCSH: Set theory. | ArithmeticFoundations.

Classification: LCC QA248 .H26 2017 | DDC 511.3/22dc23 LC record available at https://lccn.loc.gov/2016043254

Manufactured in the United States by LSC Communications

814874012017

www.doverpublications.com

Every mathematician agrees that every mathematician must know some set theory; the disagreement begins in trying to decide how much is some. This book contains my answer to that question. The purpose of the book is to tell the beginning student of advanced mathematics the basic set-theoretic facts of life, and to do so with the minimum of philosophical discourse and logical formalism. The point of view throughout is that of a prospective mathematician anxious to study groups, or integrals, or manifolds. From this point of view the concepts and methods of this book are merely some of the standard mathematical tools; the expert specialist will find nothing new here.

Scholarly bibliographical credits and references are out of place in a purely expository book such as this one. The student who gets interested in set theory for its own sake should know, however, that there is much more to the subject than there is in this book. One of the most beautiful sources of set-theoretic wisdom is still Hausdorffs Set theory. A recent and highly readable addition to the literature, with an extensive and up-to-date bibliography, is Axiomatic set theory by Suppes.

In set theory naive and axiomatic are contrasting words. The present treatment might best be described as axiomatic set theory from the naive point of view. It is axiomatic in that some axioms for set theory are stated and used as the basis of all subsequent proofs. It is naive in that the language and notation are those of ordinary informal (but formalizable) mathematics. A more important way in which the naive point of view predominates is that set theory is regarded as a body of facts, of which the axioms are a brief and convenient summary; in the orthodox axiomatic view the logical relations among various axioms are the central objects of study. Analogously, a study of geometry might be regarded as purely naive if it proceeded on the paper-folding kind of intuition alone; the other extreme, the purely axiomatic one, is the one in which axioms for the various non-Euclidean geometries are studied with the same amount of attention as Euclids. The analogue of the point of view of this book is the study of just one sane set of axioms with the intention of describing Euclidean geometry only.

Instead of Naive set theory a more honest title for the book would have been An outline of the elements of naive set theory. Elements would warn the reader that not everything is here; outline would warn him that even what is here needs filling in. The style is usually informal to the point of being conversational. There are very few displayed theorems; most of the facts are just stated and followed by a sketch of a proof, very much as they might be in a general descriptive lecture. There are only a few exercises, officially so labelled, but, in fact, most of the book is nothing but a long chain of exercises with hints. The reader should continually ask himself whether he knows how to jump from one hint to the next, and, accordingly, he should not be discouraged if he finds that his reading rate is considerably slower than normal.

This is not to say that the contents of this book are unusually difficult or profound. What is true is that the concepts are very general and very abstract, and that, therefore, they may take some getting used to. It is a mathematical truism, however, that the more generally a theorem applies, the less deep it is. The students task in learning set theory is to steep himself in unfamiliar but essentially shallow generalities till they become so familiar that they can be used with almost no conscious effort. In other words, general set theory is pretty trivial stuff really, but, if you want to be a mathematician, you need some, and here it is; read it, absorb it, and forget it.

P. R. H.

Professor of Mathematics

University of Michigan

SECTION

A pack of wolves, a bunch of grapes, or a flock of pigeons are all examples of sets of things. The mathematical concept of a set can be used as the foundation for all known mathematics. The purpose of this little book is to develop the basic properties of sets. Incidentally, to avoid terminological monotony, we shall sometimes say collection instead of set. The word class is also used in this context, but there is a slight danger in doing so. The reason is that in some approaches to set theory class has a special technical meaning. We shall have occasion to refer to this again a little later.

One thing that the development will not include is a definition of sets. The situation is analogous to the familiar axiomatic approach to elementary geometry. That approach does not offer a definition of points and lines; instead it describes what it is that one can do with those objects. The semi-axiomatic point of view adopted here assumes that the reader has the ordinary, human, intuitive (and frequently erroneous) understanding of what sets are; the purpose of the exposition is to delineate some of the many things that one can correctly do with them.

Sets, as they are usually conceived, have elements or members. An element of a set may be a wolf, a grape, or a pigeon. It is important to know that a set itself may also be an element of some other set. Mathematics is full of examples of sets of sets. A line, for instance, is a set of points; the set of all lines in the plane is a natural example of a set of sets (of points). What may be surprising is not so much that sets may occur as elements, but that for mathematical purposes no other elements need ever be considered. In this book, in particular, we shall study sets, and sets of sets, and similar towers of sometimes frightening height and complexityand nothing else. By way of examples we might occasionally speak of sets of cabbages, and kings, and the like, but such usage is always to be construed as an illuminating parable only, and not as a part of the theory that is being developed.

The principal concept of set theory, the one that in completely axiomatic studies is the principal primitive (undefined) concept, is that of belonging. If x belongs to A (x is an element of A, x is contained in A), we shall write

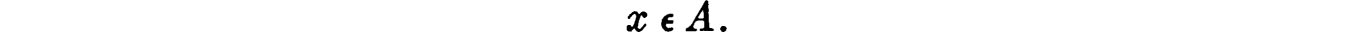
This version of the Greek letter epsilon is so often used to denote belonging that its use to denote anything else is almost prohibited. Most authors relegate to its set-theoretic use forever and use when they need the fifth letter of the Greek alphabet.