CATEGORY
THEORY
IN
CONTEXT
Emily Riehl
DOVER PUBLICATIONS, INC., Mineola, New York
of Categorical Homotopy Theory by Emily Riehl, Cambridge University Press.
Copyright 2014 by Emily Riehl
Copyright
Copyright 2016 by Emily Riehl
All rights reserved.
Bibliographical Note
Category Theory in Context is a new work, first published by Dover Publications, Inc., in 2016.
International Standard Book Number
ISBN-13: 978-0-486-80903-8
ISBN-10: 0-486-80903-X
Manufactured in the United States by RR Donnelley
80903X012016
www.doverpublications.com
To Peter Johnstone, whose beautiful Part III lectures provided my first acquaintance with category theory and form the skeleton of this book.
and
To Martin Hyland, who guided my initial explorations of this subjects frontiers and inspired my aspirations to think categorically.
The aim of theory really is, to a great extent, that of systematically organizing past experience in such a way that the next generation, our students and their students and so on, will be able to absorb the essential aspects in as painless a way as possible, and this is the only way in which you can go on cumulatively building up any kind of scientific activity without eventually coming to a dead end.
M.F. Atiyah, How research is carried out []
Contents
PREFACE
A subtle shift in perspective enables mathematical content to be described in language that is relatively indifferent to the variety of objects being considered. Rather than characterize the objects directly, the categorical approach emphasizes the transformations between objects of the same general type. A fundamental lemma in category theory implies that any mathematical object can be characterized by its universal propertyloosely by a representation of the morphisms to or from other objects of a similar form. For example, tensor products, free constructions, and localizations are characterized by universal properties in appropriate categories, or mathematical contexts. A universal property typically expresses one of the mathematical roles played by the object in question. For instance, one universal property associated to the unit interval identifies self-homeomorphisms of this space with re-parameterizations of paths. Another highlights the operation of gluing two intervals end to end to obtain a new interval, the construction used to define composition of paths.
Certain classes of universal properties define blueprints which specify how a new object may be built out of a collection of existing ones. A great variety of mathematical constructions fit into this paradigm: products, kernels, completions, free products, gluing constructions, and quotients are all special cases of the general category-theoretic notion of limits or colimits, a characterization that makes it easy to define transformations to or from the objects so-defined. The input data for these constructions are commutative diagrams, which are themselves a vehicle for mathematical definitions, e.g., of rings or algebras, representations of a group, or chain complexes.
Important technical differences between particular varieties of mathematical objects can be described by the distinctive properties of their categories: that rings have all limits and colimits while fields have few, that a continuous bijection defines an isomorphism of compact Hausdorff spaces but not of generic topological spaces. Constructions that convert mathematical objects of one type into objects of another type often define transformations between categories, called functors. Many of the basic objects of study in modern algebraic topology and algebraic geometry involve functors and would be impossible to define without category-theoretic language.
The aim of this text is to introduce the language, philosophy, and basic theorems of category theory. A complementary objective is to put this theory into practice: studying functoriality in algebraic topology, naturality in group theory, and universal properties in algebra.
Practitioners often assert that the hard part of category theory is to state the correct definitions. Once these are established and the categorical style of argument is sufficiently internalized, proving the theorems tends to be relatively easy. The relative simplicity of the proofs of major theorems occasionally leads detractors to assert that there are no theorems in category theory. This is not at all the case! Counterexamples abound in the text that follows. A short list of further significant theorems, beyond the scope of a first course but not too far to be out of the reach of comprehension, appears as an epilogue.
Sample corollaries
It is difficult to preview the main theorems in category theory before developing fluency in the language needed to state them. (A reader possessing such fluency might wish to glance ahead to .) Instead, here are a few corollaries, results in other areas of mathematics that follow trivially as special cases of general categorical results that are proven in this text.
As an application of the theory of equivalence between categories:
COROLLARY 1.5.13. In a path-connected space, any choice of basepoint yields an isomorphic fundamental group.
A fundamental lemma in category theory has the following two results as corollaries:
COROLLARY 2.2.9. Every row operation on matrices with n rows is defined by left multiplication by some nn matrix, namely the matrix obtained by performing the row operation on the identity matrix.
COROLLARY 2.2.10. Any group is isomorphic to a subgroup of a permutation group.
A special case of a general result involving the interchange of limits and colimits is:
COROLLARY 3.8.4. For any pair of sets X and Y and any function f : XY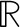
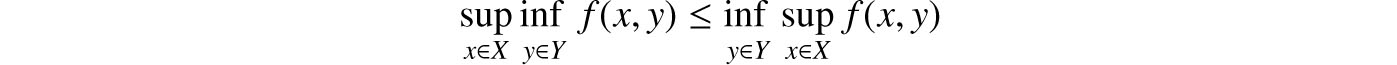
whenever these infima and suprema exist.
The following five results illustrate a few of the many corollaries of a common theorem, which describes one consequence of a type of duality enjoyed by certain pairs of mathematical constructions:
COROLLARY 4.5.4. For any function f : AB, the inverse image function f1 : PBPA between the power sets of A and B preserves both unions and intersections, while the direct image function f : PAPB only preserves unions.
COROLLARY 4.5.5. For any vector spaces U, V, W,
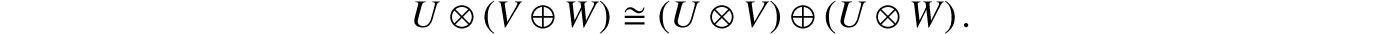
COROLLARY 4.5.6. For any cardinals , , , cardinal arithmetic satisfies the laws:
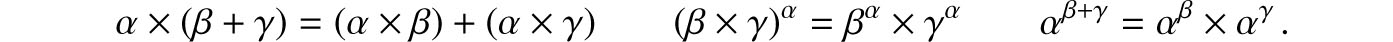
COROLLARY 4.5.7. The free group on the set X Y is the free product of the free groups on the sets X and Y.
Y is the free product of the free groups on the sets X and Y.
COROLLARY 4.5.8. For any RS bimodule M, the tensor product M Sis right exact.
Finally, a general theorem that recognizes categories whose objects bear some sort of algebraic structure has a number of consequences, including:
COROLLARY 5.6.2.













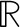
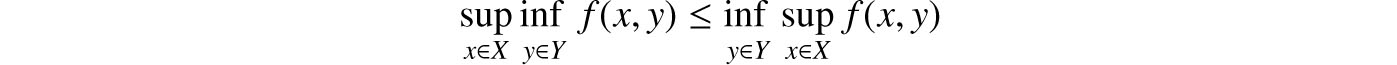
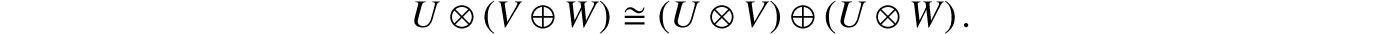
 Y is the free product of the free groups on the sets X and Y.
Y is the free product of the free groups on the sets X and Y.