Counterexamples in Analysis
Counterexamples in Analysis
Bernard R. Gelbaum
University of California, Irvine
John M. H. Olmsted
Southern Illinois University
Dover Publications, Inc.
Mineola, New York
Copyright
Copyright 1964 Holden-Day, Inc.
Copyright Renewed 1992 by Bernard R. Gelbaum and John M.H. Olmsted
All rights reserved.
Bibliographical Note
This Dover edition, first published in 2003, is an unabridged, slightly corrected republication of the 1965 second printing of the work originally published in 1964 by Holden-Day, Inc., San Francisco.
Library of Congress Cataloging-in-Publication Data
Gelbaum, Bernard R.
Counterexamples in analysis / Bernard R. Gelbaum, John M.H. Olmsted.
p. cm.
an unabridged, slightly corrected republication of the 1965 second printing of the work originally published in 1964 by Holden-Day, San Francisco [in the Mathesis series]--T.p. verso.
Includes bibliographical references and index.
ISBN-13: 978-0-486-42875-8
ISBN-10: 0-486-42875-3
1. Mathematical analysis. I. Olmsted, John Meigs Hubbell, 1911-II. Title.
QA300.G4 2003
515dc21
2002041784
Manufactured in the United States by Courier Corporation
42875307
www.doverpublications.com
Preface
The principal type of question asked in mathematics is, Is statement S true? where the statement S is of the form Every member of the class A is a member of the class 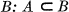 . To demonstrate that such a statement is true means to formulate a proof of the inclusion
. To demonstrate that such a statement is true means to formulate a proof of the inclusion  . To demonstrate that such a statement is false means to find a member of A that is not a member of B, in other words a counterexample. To illustrate, if the statement S is Every continuous function is somewhere differentiable, then the sets A and B consist of all continuous functions and all functions that are somewhere differentiable, respectively; Weierstrasss celebrated example of a function f that is continuous but nowhere differentiable (cf. ) is a counterexample to the inclusion
. To demonstrate that such a statement is false means to find a member of A that is not a member of B, in other words a counterexample. To illustrate, if the statement S is Every continuous function is somewhere differentiable, then the sets A and B consist of all continuous functions and all functions that are somewhere differentiable, respectively; Weierstrasss celebrated example of a function f that is continuous but nowhere differentiable (cf. ) is a counterexample to the inclusion 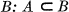 , since f is a member of A that is not a member of B. At the risk of oversimplification, we might say that (aside from definitions, statements, and hard work) mathematics consists of two classesproofs and counter-examples, and that mathematical discovery is directed toward two major goalsthe formulation of proofs and the construction of counterexamples. Most mathematical books concentrate on the first class, the body of proofs of true statements. In the present volume we address ourselves to the second class of mathematical objects, the counterexamples for false statements.
, since f is a member of A that is not a member of B. At the risk of oversimplification, we might say that (aside from definitions, statements, and hard work) mathematics consists of two classesproofs and counter-examples, and that mathematical discovery is directed toward two major goalsthe formulation of proofs and the construction of counterexamples. Most mathematical books concentrate on the first class, the body of proofs of true statements. In the present volume we address ourselves to the second class of mathematical objects, the counterexamples for false statements.
Generally speaking, examples in mathematics are of two types, illustrative examples and counterexamples, that is, examples to show why something makes sense and examples to show why something does not make sense. It might be claimed that any example is a counterexample to something, namely, the statement that such an example is impossible. We do not wish to grant such universal interpretation to the term counterexample, but we do suggest that its meaning be sufficiently broad to include any example whose role is not that of illustrating a true theorem. For instance, a polynomial as an example of a continuous function is not a counterexample, but a polynomial as an example of a function that fails to be bounded or of a function that fails to be periodic is a counterexample. Similarly, the class of all monotonic functions on a bounded closed interval as a class of integrable functions is not a counterexample, but this same class as an example of a function space that is not a vector space is a counterexample.
The audience for whom this book is intended is broad and varied. Much of the material is suitable for students who have not yet completed a first course in calculus, and for teachers who may wish to make use of examples to show to what extent things may go wrong in calculus. More advanced students of analysis will discover nuances that are usually by-passed in standard courses. Graduate students preparing for their degree examinations will be able to add to their store of important examples delimiting the range of the theorems they have learned. We hope that even mature experts will find some of the reading new and worthwhile.
The counterexamples presented herein are limited almost entirely to the part of analysis known as real variables, starting at the level of calculus, although a few examples from metric and topological spaces, and some using complex numbers, are included. We make no claim to completeness. Indeed, it is likely that many readers will find some of their favorite examples missing from this collection, which we confess is made up of our favorites. Some omissions are deliberate, either because of space or because of favoritism. Other omissions will undoubtedly be deeply regretted when they are called to our attention.
This book is meant primarily for browsing, although it should be a useful supplement to several types of standard courses. If a reader finds parts hard going, he should skip around and pick up something new and stimulating elsewhere in the book. An attempt has been made to grade the contents according to difficulty or sophistication within the following general categories: (i) the chapters, (ii) the topics within chapters, and (iii) the examples within topics. Some knowledge of related material is assumed on the part of the reader, and therefore only a minimum of exposition is provided. Each chapter is begun with an introduction that fixes notation, terminology, and definitions, and gives statements of some of the more important relevant theorems. A substantial bibliography is included in the back of the book, and frequent reference is made to the articles and books listed there. These references are designed both to guide the reader in finding further information on various subjects, and to give proper credits and source citations. If due recognition for the authorship of any counterexample is lacking, we extend our apology. Any such omission is unintentional.
Finally, we hope that the readers of this book will find both enjoyment and stimulation from this collection, as we have. It has been our experience that a mathematical question resolved by a counterexample has the pungency of good drama. Many of the most elegant and artistic contributions to mathematics belong to this genre.
B.R.G.
Irvine, California
J.M.H.O.
Carbondale, Illinois
Part I
Functions of a Real Variable
Chapter 1
The Real Number System
Introduction
We begin by presenting some definitions and notations that are basic to analysis and essential to this first chapter. These will be given in abbreviated form with a minimum of explanatory discussion. For a more detailed treatment see ] of the Bibliography.
If A is any set of objects, the statement a is a member of A is written 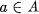 . The contrary statement that a is not a member of A is written
. The contrary statement that a is not a member of A is written 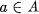 . If A and B are sets, the statement A is a subset of B is written
. If A and B are sets, the statement A is a subset of B is written 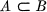
Next page












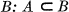 . To demonstrate that such a statement is true means to formulate a proof of the inclusion
. To demonstrate that such a statement is true means to formulate a proof of the inclusion  . To demonstrate that such a statement is false means to find a member of A that is not a member of B, in other words a counterexample. To illustrate, if the statement S is Every continuous function is somewhere differentiable, then the sets A and B consist of all continuous functions and all functions that are somewhere differentiable, respectively; Weierstrasss celebrated example of a function f that is continuous but nowhere differentiable (cf. ) is a counterexample to the inclusion
. To demonstrate that such a statement is false means to find a member of A that is not a member of B, in other words a counterexample. To illustrate, if the statement S is Every continuous function is somewhere differentiable, then the sets A and B consist of all continuous functions and all functions that are somewhere differentiable, respectively; Weierstrasss celebrated example of a function f that is continuous but nowhere differentiable (cf. ) is a counterexample to the inclusion 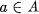 . The contrary statement that a is not a member of A is written
. The contrary statement that a is not a member of A is written