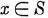Maxwell Rosenlicht - Introduction to Analysis

Introduction to Analysis

Introduction to Analysis

by

MAXWELL ROSENLICHT

University of California at Berkeley

DOVER PUBLICATIONS, INC.

New York

Copyright 1968 by Maxwell Rosenlicht

All rights reserved.

This Dover edition, first published in 1986, is an unabridged and unaltered republication of the work first published by Scott, Foresman and Company, Glenview, Illinois, in 1968.

Library of Congress Cataloging-in-Publication Data

Rosenlicht, Maxwell.

Introduction to analysis.

Reprint. Originally published: Glenview, 111. : Scott, Foresman, and Co., 1968.

Bibliography: p.

Includes index.

1. Mathematical analysis. I. Title.

QA300.R63 1986 515 85-25300

ISBN 0-486-65038-3 (pbk.)

Manufactured in the United States by Courier Corporation

65038313

www.doverpublications.com

This text is the outgrowth of a course given at Berkeley since 1960. The object is to redo calculus correctly in a setting of sufficient generality to provide a reasonable foundation for advanced work in various branches of analysis. The emphasis is on abstraction, concreteness, and simplicity. A few abstract ideas are introduced, almost minimal in number. Such important concepts as metric space, compactness, and uniform convergence are discussed in such a manner that they will not need to be redone later. They are given concrete illustration and their worth is demonstrated by using them to prove the results of calculus, generalized in ways that are obviously meaningful and practical.

The background recommended is any first course in calculus, through partial differentiation and multiple integrals (although, as a matter of fact, nothing is assumed except for the axioms of the real number system). A person completing most of the material in this book should not only have a respectable comprehension of basic real analysis but should also be ready to take serious courses in such subjects as integration theory, complex variable, differential equations, other topics in analysis, and general topology. Experience indicates that this material is accessible to a wide range of students, including many with primary interests outside mathematics, provided there is a stress on the easier problems.

The quest for simplicity has resulted in the elimination of a host of mathematical synonyms and the omission or relegation to the problem sets of a number of important ideas. Some problems, easily recognizable, assume a familiarity with linear algebra that was considered unwise to presume of all students. Indeed only a few simple facts on determinants are needed for the chapters on multivariable calculus, but things are so arranged that the instructor who wishes to avail himself of the conveniences of linear algebra may easily do so with no break in continuity. Differential forms were excluded, regrettably, to avoid exorbitant algebraic detours.

This text can be used for courses ranging in length from one to two quarters. The original semester course at Berkeley covered the first eight chapters, with the omission of most of the third section of the eighth chapter. At present Berkeley has a two-quarter sequence with the first quarter, somewhat sped up, covering the first six chapters and parts of the seventh.

Here are some comments on the individual chapters. Chapter I, which discusses material on basic set theory that is familiar to many students, can be covered very rapidly. Chapter II gives a brief account of how all the properties of the real numbers can be deduced from a few axioms. This material can also be covered rapidly. It should not be bypassed, however, for contrary to a widespread faith in modern pedagogy, my experience has been that time spent here is not wasted. Chapters III and IV, on metric spaces and continuous functions, are the meat of the book. They must be done with great care. After this, Chapters V, VI, and VII flow along smoothly, for their substance (elementary calculus) is familiar and the proofs now make sense. Chapter VIII, which is about existence theorems, is of a slightly greater order of difficulty. One may save some time by going very lightly over the implicit function theorem if it is intended to do the general case later, in the following chapter. The last section of the chapter treats ordinary differential equations, and the classroom discussion of these may with relative impunity be restricted to the very first theorem. Chapters IX and X, on multivariate calculus, conclude the book. They should cause no difficulty for anyone who has come this far. However, omitting them entirely would be preferable to an attempt to rush through.

It is impossible to write a text such as this without an obvious indebtedness to J. Dieudonns classic Foundations of Modern Analysis. My gratitude is also due my colleagues of the curricular reform committee at Berkeley which instituted the new Mathematics 104 course, to Mrs. Sandra Cleveland for writing up my original lectures, to Adam Koranyi, whose revised notes have long been in use, for many conversations, to numerous other colleagues and students for their comments, to my family for its patience, and to Scott, Foresman and Company for its affable efficiency.

Contents

Introduction to Analysis

Set theory is the language of mathematics. The most complicated ideas in modern mathematics are developed in terms of the basic notions of set theory. Fortunately the grammar and vocabulary of set theory are extremely simple, at least in the sense that it is possible to go very far in mathematics with only a small amount of set theory. It so happens that the subject of set theory not only underlies mathematics but has become itself an extensive branch of study; however we do not enter deeply into this study because there is no need to. All we must do here is familiarize ourselves with some of the basic ideas so that the language may be used with precision. A first reading of this chapter can be very rapid since it is mainly a matter of getting used to a few words. There is occasional verbosity, directed toward the clarification of certain simple ideas which are really somewhat more subtle than they appear.

We do not attempt to define the word set. Intuitively a set is a collection, or aggregate, or family, or ensemble (all of which words are used synonymously with set) of objects which are called the elements, or members of the set, and the set is completely determined by the knowledge of which objects are elements of it. We may speak, for example, of the set of students at a certain university; the elements of this set are the individual students there. Similarly we may speak of the set of all real numbers (to be discussed in some detail in the next chapter), or the set of all straight lines in a given plane, etc. It should be noted that the elements of a set may themselves be sets; for example each element of the set of all straight lines in a given plane is a set of points, and we may also consider such less mathematical examples as the set of married couples in a given town, or the set of regiments in an army.

We shall generally use capital letters to denote sets and lower-case letters to denote their elements. The symbol is used to denote membership in a set, so that