Konrad Knopp - Elements of the Theory of Functions

Elements of the

THEORY OF FUNCTIONS

KONRAD KNOPP

Translated by

FREDERICK BAGEMIHL

DOVER PUBLICATIONS, INC.

Mineola, New York

Copyright

Copyright 1952, 1980 by Dover Publications, Inc.

All rights reserved.

Bibliographical Note

This Dover edition, first published in 1952 and reissued in 2016, is a new English translation of Elemente der Funktionentheorie.

Library of Congress Catalog Card Number: 53-7031

International Standard Book Number

ISBN-13: 978-0-486-60154-0

ISBN-10: 0-486-60154-4

Manufactured in the United States by RR Donnelley

60154420 2016

www.doverpublications.com

CONTENTS

Elements of the

THEORY OF FUNCTIONS

SECTION I COMPLEX NUMBERS AND THEIR GEOMETRIC REPRESENTATION

CHAPTER I

FOUNDATIONS

1. Introduction

The name Theory of Functions is used to denote all those investigations which arise if one seeks to transfer the problems and methods of real analysis (i.e., differential and integral calculus, and related fields) to the case in which all numerical quantities (constants, independent and dependent variables) that appear are permitted to be complex numbers, that is, numbers of the form 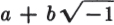. Early and quite automatically such considerations forced their way into investigations connected with various problems in real analysis, and have been carried out, in conjunction with the solution of these problems, in the course of centuries,hesitantly at first, but soon with ever greater success (see for further details). Today the theory of functions is one of the most extensive and important branches of higher mathematics.

In these Elements of the Theory of Functions we shall treat only those topics which are simplest, but which are at the same time most important for the further development of the theory.concept of sets of numbers, the limit concept, and closely related matters, in particular the theory of infinite series, are extended to complex quantities, or, as we say briefly, to the complex domain. Further, we shall carry over the notion of function and its most important properties to the case in which independent and dependent variables are complex. When combined with the limit concept, this yields the foundations of a differential calculus for functions of a complex variable. Finally, we shall study more closely the so-called elementary functions, including the rational, and, in particular, the linear, functions, the exponential function, the trigonometric functions, and several others, as well as their inverses, such as the logarithm and the cyclometric functions. The extension of the integral calculus to the complex domain, however, is not regarded as belonging properly to the elements of the theory of functions.

We shall see () that the operations performed on complex numbers, and, eventually, that all the investigations just mentioned, can be visualized, in a number plane or on a number sphere, even more vividly than in the real domain, This forms the content of that part of our theory which is called geometric theory of functions.

It is evident from what has been said, that in order to be able to understand this little book, a knowledge of the foundations of real analysis and of the elements of analytic geometry is indispensable, inasmuch as the extension to the complex domain is accomplished after the pattern of real analysis, and use is made of simple geometric facts for purposes of visualization. So as to have a fixed point of departure, we shall state in what is most fundamental as regards the construction of analytic geometry.

2. The system of real numbers

We presuppose familiarity with the system of real numbers, of course, as far as its practical use is concerned; but because of its fundamental importance, we shall present briefly here the essential ideas which lead to its construction.

The starting point of all investigations concerning numbers is the sequence of natural numbers, 1, 2, 3, ..., and the two operations on them: addition and multiplication. The necessity of performing the inverses of these operations presently compels the introduction of 0 (zero), negative numbers, and, finally, fractions. The totality of integral, fractional, positive and negative numbers, and zero, is called the system of (real) rational numbers.

One can operate with these numbers, which are now denoted for brevity by single Roman letters, according to certain rules which are called the fundamentals laws of arithmetic. These are the following, in which by numbers we mean, for the present, only the rational numbers just referred to:

I. F UNDAMENTAL LAWS OF EQUALITY AND ORDER

1. The set of numbers is an ordered set; i.e., if a and b are any numbers, they satisfy one, and only one, of the relations

This order obeys these additional laws:

2. a = a for every number a.

3. a = b implies b = a.

4. If a = b and b = c, then a = c.

5. If ab and b < c, or if a < b and bc, then a < c.

All numbers which are greater than zero are called positive, all numbers which are less than zero are called negative. If a number is equal to zero, we also say that it vanishes.

II. F UNDAMENTAL LAWS OF ADDITION

1. Every pair of numbers a and b can be added; the symbol (a + b) or a + b always represents a definite number, the sum of a and b.

This formation of sums obeys these laws:

2. If a = aand b = b, then a + b = a + b. (If equals are added to equals, the sums are equal.)

3. a + b = b + a. (Commutative law.)

4. (a + b) + c = a + (b + c). (Associative law.)

5. a < b implies a + c < b + c. (Monotonic law.)

III. F UNDAMENTAL LAW OF SUBTRACTION

The inverse of addition can always be performed; i.e., if a and b are any numbers, there exists a numberx such that a + x = b.

The number x thus determined is called the difference of b and a, and is denoted by (ba).

IV. F UNDAMENTAL LAWS OF MULTIPLICATION

1. Every pair of numbers a and b can be multiplied; the symbol ab or ab always represents a definite number, the product of a and b.

This formation of products obeys these laws:

2. If a = aand b = b, then ab = ab. (If equals are multiplied by equals, the products are equal.)

3. ab = ba. (Commutative law.)

4. (ab)c = a(bc). (Associative law.)

5. (a + b)c = ac + bc. (Distributive law.)

6. If a < b, and c > 0, then ac < bc. (Monotonic law.)

The four rules of sign and, as a supplement to them, the result that

follow in the simplest fashion, but certainly as demonstrable facts, from the fundamental laws enumerated thus far. The four rules of sign assert, in particular, that