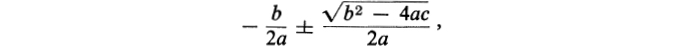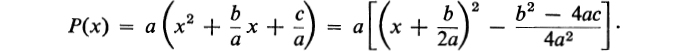John W. Dettman - Applied Complex Variables

Applied Complex Variables

John W. Dettman

Professor of Mathematics, Oakland University

DOVER PUBLICATIONS, INC.
New York

Copyright 1965 by John W. Dettman.

All rights reserved.

This Dover edition, first published in 1984, is an unabridged and unaltered republication of the fifth printing, 1970, of the work first published by The Macmillan Company, N.Y., in 1965.

Library of Congress Cataloging in Publication Data

Dettman, John W. (John Warren) Applied complex variables.

Reprint. Originally published: New York : Macmillan, 1965.

Bibliography: p.

Includes index.

1. Functions of complex variables. I. Title.

QA331.D55 1984 515.9 83-20604

eISBN-13: 978-0-486-15828-0

Manufactured in the United States by Courier Corporation
64670X12 2014
www.doverpublications.com

There was a time when the mathematical needs of most engineers and physicists were fairly well met with a routine calculus course followed by an elementary course in ordinary differential equations. But nothing stands still, least of all science and mathematics. Now, we hear it suggested that every good engineer or physicist should know topics from advanced calculus, complex analysis, ordinary and partial differential equations, boundary value problems, Fourier and Laplace transforms, integral equations, asymptotic expansions, linear algebra, probability, statistics, numerical analysis, and so on. Thus a large body of mathematics which was formerly treated only in advanced mathematics books has become the province of engineers and physicists. This book is an attempt to make accessible to a larger audience a certain number of those topics which seem to be a natural outgrowth of the study of analytic functions of a complex variable.

Most students of applied mathematics want to get as quickly as possible to the applications. There is a danger in this, however, for if the foundation is weak the structure will be shaky and will not support further building. On the other hand, the student must be well motivated to make the effort to master the fundamentals and should not be thwarted in his goal to study the applications by too many frills. With this in mind, the book has been divided into two parts. The first part deals with the fundamentals of analytic function theory and should be studied sequentially before going on to the second part which deals with the applications of analytic function theory. The second part introduces five of the major applications, more or less independently of one another. In other words, once the first half of the book is mastered, one can pick any one of the five applications to study in detail. This makes it possible for the book to be used for a one-semester course, where one or more applications can be introduced, depending on the time available, or for a two-semester course, in which virtually all the applications are studied.

Although a fairly brisk pace is maintained throughout, I have assumed no advanced calculus background. A well-motivated student with a modern calculus course behind him should be able to study this material with profit. This should make it possible to use the book for a junior- or senior-level advanced engineering mathematics course or for an undergraduate introduction to complex variables for mathematics majors.

Complex analysis is a traditional subject going back to Cauchy and Riemann in the nineteenth century. Therefore, it would be impossible to cite original sources for the material in this book. For the benefit of the reader a list of references is included at the end.

The author is indebted to many for help in the completion of this work, not the least of whom is Professor Bernard Epstein of the University of New Mexico who read a large part of the manuscript and made many helpful suggestions. About one-third of the manuscript was written while the author was supported by a National Science Foundation fellowship at New York University.

JOHN W. DETTMAN
Oakland University
Rochester, Michigan

Applied Complex Variables

Probably the first time a school child comes across the need for any kind of number other than the real numbers is in an algebra course where he studies the quadratic equation ax2 + bx + c = 0. He is shown by quite elementary methods that the roots of this equation must be of the form

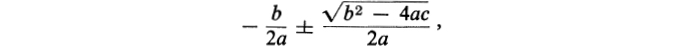
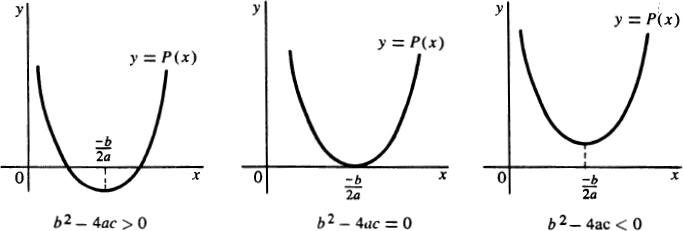
the usual quadratic formula. He is then told that if the discriminant b2 4ac 0, then the roots of the quadratic equation are real. Otherwise, they are complex. It must seem very strange to the student, who has known only the real numbers and is told that a, b, c, and x in the equation are real, that he must be confronted with this strange new beast, the complex number. Actually, the difficulty could be avoided if the problem were stated in the following way: For what real values of x does the polynomial P(x) = ax2 + bx + c, with a, b, and c real, and a 0, take on the value zero? Then P(x) can be written as follows:

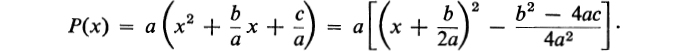
Obviously, since (x + b/2a)2 and 4a2 are nonnegative, if b2 4ac < 0, then P(x) is never zero, and the answer, in this case, is that there are no real values of x for which P(x) = 0. The notion of a complex number need not enter the discussion. Furthermore, if the student has any notion of the graph of a function, then there is an obvious geometrical picture which makes the situation quite clear. Let us assume, without loss of generality, that a > 0. Then, clearly, P(x) takes on a minimum value of (4acb2)/4a when x = (b/2a). If b2 4ac > 0, there are two zeros of P(x), if .

Actually, the discussion of complex roots of the quadratic equation need not come up at all unless we are trying to answer the more difficult question: For what values of the complex variable z does the polynomial P(z) = az2 + bz + c take on the value zero? Here, a, b, and c may be complex numbers. But this plunges us into the heart of our subject and raises many interesting questions: What is a complex number? What is a function of a complex variable? What are some of the more interesting properties of functions of a complex variable? Do polynomial functions have zeros? (Fundamental Theorem of Algebra), and so on. In trying to answer these questions and others which will most certainly come up, we shall uncover a very rich branch of mathematics, which has and will have far reaching implications and great applicability to other branches of science.