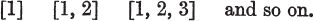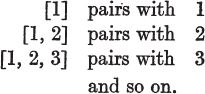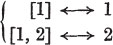H. A. Thurston - The Number System

THE NUMBER
SYSTEM

H. A. THURSTON

DOVER PUBLICATIONS, INC.

MINEOLA, NEW YORK

Copyright

Copyright 1956 by H. A. Thurston
All rights reserved.

Bibliographical Note

This Dover edition, first published in 1967 and republished in 2007, is a slightly corrected republication of the The Number-System, which was originally published by Blackie and Son, Ltd., London, and Interscience Publishers, New York, in 1956.

International Standard Book Number: eISBN-13: 978-0-486-15494-7

Manufactured in the United States of America
Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y 11501

PREFACE

I T IS NOT NECESSARY TO BE A WATCH-MAKER TO BE able to tell the time. Nor is it necessary to study the foundations of arithmetic in order to carry out the calculations required in everyday life, in science, or in mathematics. This book, however, is intended for those whose aim is to understand arithmetic rather than to put it to a practical use.

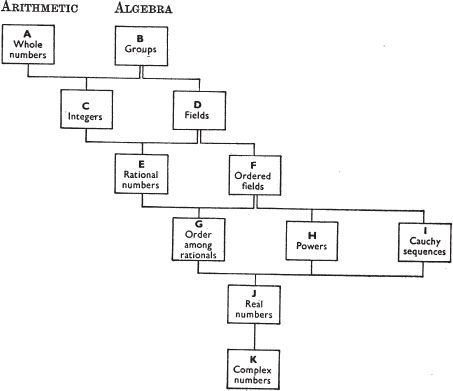
The systematic part of the book is the second part, and consists of Chapters A-K. It is complete in itself, and presents a detailed construction of the number-system, starting from Peanos axioms. Chapters A-G comprise a development of the rational number-system, and the detail is deliberately very full; every step, no matter how trivial, being justified by a reference to the theorem or lemma used. In Chapters H-K, first the theory of powers of rational numbers and then the real and complex number-systems are developed. Here the references are not quite so painstaking, the ordinary laws of arithmetic for rational numbers being freely used, as well as such familiar abbreviations as x + y + z for (x + y) + z.

In order to keep the bulk of the second part of the book within bounds, explanatory matter has been cut to a minimum; but the first part of the book consists of explanatory chapters () whose function is to explain and comment on the axioms and definitions, and to make the treatment in the second part digestible. The thoughtful non-mathematical reader who wants to know something about the number-system of modern mathematics without going deeply into the details could profitably read these chapters with perhaps a glance at the definitions and the statements of the theorems in the systematic part. But the reader for whom the book is primarily intended is the student of mathematics. He should read both parts, and probably the best order to take them in is as follows: I, II, A, III, IV, V, B, VI, C, D, E, F, G, VII, VIII, H, I, J, IX, K, X, XI.

The exercises are to help the reader to confirm that he has assimilated the ideas and to give him practice in using the concepts introduced, rather than to test his technique and industry. In general, solutions to the exercises should be strict; there is no point in proving that 2 + 2 = 4 unless this is properly done. But some illustrative exercises may be solved more freely. These are marked with asterisks.

A certain amount of pure algebra is introduced, partly for economy (the algebraic theorems being applied two or more times), partly to bring out the analogy between different parts of the arithmetical system, and partly to illustrate one use of abstract mathematics. The systematic chapters are for the most part alternately arithmetical and algebraic; the following chart shows their interdependence.

CONTENTS

Part I

EXPLANATORY TREATMENT

CHAPTER I

Counting

. Numbers are used for counting; that is to say, for comparing the many-fold-ness of groups of objects. If we want to know whether there are more states in the United States than counties in England, the obvious thing to do is to count first the states and then the English counties. But the most obvious process is not in fact the simplest. We can see at a glance that there are more dots in [..] than in []. Some animals can distinguish between groups of different sizes (e.g. between a group of three men going into a hut, and a group of two of them coming out again), but there is no evidence that they can count.

The difference between counting and comparison without counting is brought out clearly if we imagine a primitive tribe whose language contains no numbers above 20. The tribesmen can then distinguish between groups of 17 and of 18 by counting, but not between groups of 25 and of 75. By the comparison method, on the other hand, the 25 and the 75 are far more easily distinguished than are the 17 and the 18. Comparison does not, however, depend on merely looking at the two groups. The crude method can be refined.

One set is of smaller size than another if and only if it is matchable with a set consisting of some members of the second set, but is not matchable with the second set itself.

. A peasant farmer will perhaps be able to tell infallibly when one cow is more valuable than another. A more sophisticated merchant will not be content with this; he will want their values in terms of money. In other words, he wants a standard scalethe scale of money-valuesinstead of mere comparisons. We can construct a scale for our sizes-of-sets.

Consider [.], [..], [], [.], and so on. If a set is matchable with the set of dots in [.], we say that the number of members of the set is one. If it is matchable with the set of dots in [..], the number is two. Similarly for three, four, and higher numbers. We have now practically reached the stage of counting: counting is simply replacing the rather clumsy standard set by signs. The trick is to use a set of signs arranged in a fixed order. Let us suppose that we use the familiar signs 1, 2, 3, 4, etc. Then for our standard sets we take, not sets of dots, but sets of these signs, in the fixed order

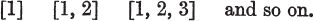
When we match a set of objects against one of the standard sets, we do not need to remember the whole standard set: it is enough to know which is the last number in it. Now at last we are really counting. We have used the fact that the set of standard sets is matchable with the set of number-signs, and have replaced each standard set by the number-sign with which it is paired. The matching can be illustrated thus:

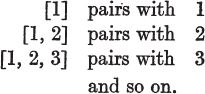
Usually, matchings are written in the form

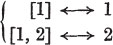
or by a general formula such as [1, 2, , n] n.

1 and 2 are the mates of [1] and of [1, 2] respectively.

. I want to emphasize that all we need for counting is a set of signs in a fixed order going on for ever. (Clearly the set must not ever come to an end: if it did we should not be able to count sets larger than the set of available signs.) The signs may be words:

That in our familiar systemthe decimal systemwe have only a small number of simple signs (1 to 9 and 0), using compound signs (10, 11, , 100, ) for bigger numbers, is only a matter of convenience of writing. Calculation with these signsthe process taught at school as arithmeticis really the study of the decimal notation rather than the study of