Romanowicz - 100 math brainteasers: Arithmetic, Algebra, and Geometry Brain Teasers, Puzzles, Games, and Problems with Solutions

CHAPTER 1

NATURAL NUMBERS AND INTEGERS

1. AT THE BOOKSTORE

Agatha was going to buy eight books, but it turned out she was $7 short. What she did was buy just seven books and was left with $5 to spare. How much did a single book cost if all the titles she was interested in cost the same?

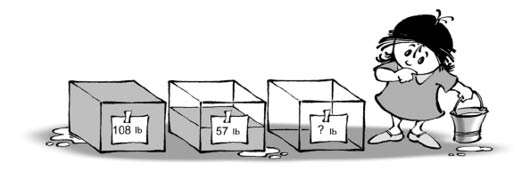
2. AQUARIUM

A cuboidal glass aquarium filled to the brim with water weighs 108 lb. The very same vessel half filled weighs 57 lb. How much does the empty aquarium weigh?

3. MULTIPLYING THE SPOTS

In the figure below, find the mystery domino tile which yields a correct operation of multiplication of a three-digit number by a one-digit number, and whose product equals 2532?

4. THE YEAR OF SOPHIES BIRTH

In January 1993, Sophies age equaled the sum of digits comprised in her birth year. What year was Sophie born in?

5. I WILL NOT BE A TRIANGLE!

Kate has found six two-digit numbers, such that no three of them can constitute the lengths of a triangles sides.

Can you find such numbers?

Reminder: Given that a, b, c > 0 are the lengths of a certain triangle, if a + b > c, b + c > a, and c + a > b, then the length of any side of the triangle is smaller than the sum of the lengths of the two remaining sides.

6. A MEASURE OF SUGAR

With a double pan scale and only four weights of 1-oz, 3-oz, 9-oz, and 27-oz, how does one measure 15 oz of sugar, and then 25 oz?

7. RIDDLE MAN

When Augustus de Morgan (a mathematician who was born and died in the 19 th century) was asked about his age, he replied: I was x years old in the year x .

What year was he born in? Could such a strange lot have befallen someone who was born and died in the 20 th century?

8. WHAT DID TOM WRITE?

Tom wrote down two positive integers consisting of the following digits: 1, 2, 3, 4, 5, and 6. Each of the digits appeared in only one of the two numbers, and only once. When Tom added up these numbers, he obtained 750. What positive integers did Tom write?

9. NINE-DIGIT NUMBERS

Out of the digits 1, 2, 3, 4, 5, 6, 7, 8, and 9, a nine-digit number was formed in which each of the digits enumerated occurred only once, and in addition, each digit was either greater by 5 or smaller by 4 than the preceding one. How many such numbers can be formed?

10. PUPILS AND GEOMETRY

The teacher gave her Class-five pupils a difficult geometry problem to solve. It turned out that the number of boys who solved it was greater by one than the number of girls who failed to do so. Which group outnumbered the other: All the pupils that solved the problem or all the girls?

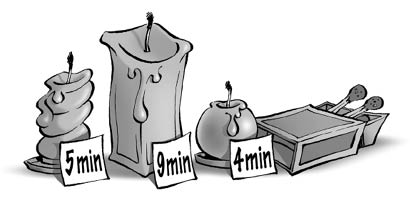
11. WAX CLOCKS

We are given three candles, the first of which burns out in 4 minutes, the second one in 5 minutes, and the third in 9 minutes. How can we possibly measure 6 minutes by lighting and blowing out the candles? Our assumption holds that both lighting and blowing out take place instantly.

12. A PECULIAR NUMBER SEQUENCE

Does a sequence of 11 integers other than zero exists and whose sum of seven successive terms is always positive, whereas the sum of all its terms is a negative number?

Clue: Does an a , b , c three-term sequence exist in which a + b + c < 0, but a + b > 0 and b + c > 0?

13. DOTS ON THE SIDES

Ann and Kate are sitting face to face and are looking at a big die lying between them. Each girl sees the upper side of the dice and only two of the four lateral sides, but neither sees the same lateral ones. Ann has counted 10 dots on the three sides she is facing, whereas Kate sees 14 dots on the sides in front of her. How many dots are there on the side unseen by the girls?

Note: The sum of dots on opposite sides is always 7.

14. ABSENT-MINDED JOAN

Joan was helping her aunt run a candy shop. When the shop closed after a days work, the girl counted all the chocolate bars that remained on the shelves, but due to her absent-mindedness, the number she wrote down in her notebook was missing its final digit. The following morning, her aunt found to her surprise that the number of chocolate bars on the shelves was greater by 89 than the number found in Joans notebook. What was the number Joan should have written down?

15. A MATTER OF AGE

Two sisters, Barbara and Monica, celebrate their birthday together since they were born on the same day and in the same month, except that Barbara is two years younger than Monika. To a tactless question about her age, Monica replied with a smile: Barbara is very young she is not as old as we were together nine years ago. As for me, I am very old, because I am older than we were together nine years ago.

How old is each sister now?

16. NEW YORK HAS THE UPPER HAND!

The final score of the hockey game between the New York Islanders and the Boston Bruins was 9 to 5. Is it possible that partway through the game, there must have come a moment in which the Bruins had exactly the same number of goals as the Islanders scored in the remainder of the game?

17. A CHOCOLATE PROBLEM

A shopkeeper has 30 chocolate bars, each of which weighs 2, 3, or 4 ounces. The total weight of the bars is 100 ounces. Which bars does the shopkeeper have more: 2 or 4-oz bars?

18. KINGLETS

A certain king has numerous offspring. His eldest son is a twin, and the remaining children apart from seven are also twins. In addition, all the kings children are triplets except those seven. How many children does the king have?