Presh Talwalkar - Math Puzzles Volume 3: Even More Riddles And Brain Teasers In Geometry, Logic, Number Theory, And Probability

Copyright Presh Talwalkar

About The Author

Presh Talwalkar studied Economics and Mathematics at Stanford University. His site Mind Your Decisions has blog posts and original videos about math that have been viewed millions of times.

Books By Presh Talwalkar

The Joy of Game Theory: An Introduction to Strategic Thinking . Game Theory is the study of interactive decision-making, situations where the choice of each person influences the outcome for the group. This book is an innovative approach to game theory that explains strategic games and shows how you can make better decisions by changing the game.

Math Puzzles Volume 1: Classic Riddles And Brain Teasers In Counting, Geometry, Probability, And Game Theory . This book contains 70 interesting brain-teasers.

Math Puzzles Volume 2: More Riddles And Brain Teasers In Counting, Geometry, Probability, And Game Theory . This is a follow-up puzzle book with more delightful problems.

Math Puzzles Volume 3: Even More Riddles And Brain Teasers In Geometry, Logic, Number Theory, And Probability . This is the third in the series with 70 more problems.

But I only got the soup! This fun book discusses the mathematics of splitting the bill fairly.

40 Paradoxes in Logic, Probability, and Game Theory . Is it ever logically correct to ask May I disturb you? How can a football team be ranked 6th or worse in several polls, but end up as 5th overall when the polls are averaged? These are a few of the thought-provoking paradoxes covered in the book.

Multiply By Lines . It is possible to multiply large numbers simply by drawing lines and counting intersections. Some people call it how the Japanese multiply or Chinese stick multiplication. This book is a reference guide for how to do the method and why it works.

The Best Mental Math Tricks . Can you multiply 97 by 96 in your head? Or can you figure out the day of the week when you are given a date? This book is a collection of methods that will help you solve math problems in your head and make you look like a genius.

Why You Should Study Math Puzzles

This is the third book I am publishing about mathematical brain teasers and riddles. What is the point of all of these math problems?

From a practical perspective, math puzzles can help you get a job. They have been asked during interviews at Google, Goldman Sachs, as well as other tech companies, investment banks, and consulting firms.

Math puzzles also serve a role in education. Because puzzles illustrate unexpected solutions and can be solved using different methods, they help students develop problem solving skills and demonstrate how geometry, probability, algebra, and other topics are intimately related. Math puzzles are also great for practice once you are out of school.

But mostly, math puzzles are worthwhile because they are just fun. I like to share these problems during parties and holidays. Even people who do not like math admit to enjoying them. So with that, I hope you will enjoy working through this collection of puzzles as much as I have enjoyed preparing the puzzles and their solutions.

This book is organized into easy, medium, and hard puzzles. It is never easy to organize puzzles by difficulty: some of the hard puzzles may be easy for you to solve and vice versa. But as a whole, the harder puzzles tend to involve higher-level mathematics, like knowledge of probability distributions or calculus.

Each puzzle is immediately accompanied with its solution, as I have done in the other two math puzzle ebooks. I have never been a fan of how print books put all the solutions at the end--it is too easy to peek at the solution for another problem's solution by mistake. In any case, while you are working on a problem, avoid reading the following section which contains the solution.

Table of Contents

?

Part I: Easy Puzzles

Puzzle 1: Triangle Ratios

A circle is inscribed in an equilateral triangle. Then an equilateral triangle is drawn inside the circle, as pictured below.

What is the ratio of the area of the smaller equilateral triangle to the larger equilateral triangle?

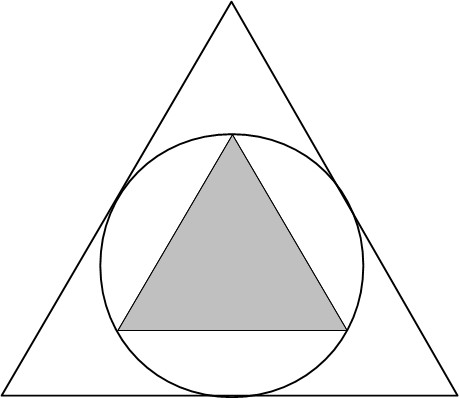
Answer To Puzzle 1: Triangle Ratios

There's no need to do complicated calculations. The easiest way is to rotate the triangle inside the circle to get the following figure.

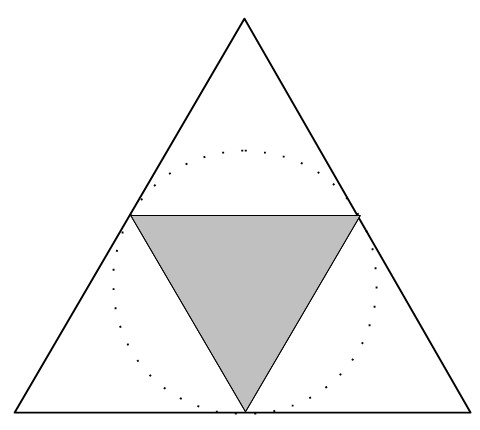
Now the answer is obvious! The large equilateral triangle is divided into 4 small equilateral triangles: three of them are facing "up" while the shaded one is facing "down." Since 4 small equilateral triangles make up the 1 large equilateral triangle, the shaded triangle is 1/4 the area of the larger equilateral triangle.

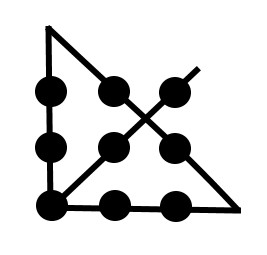
Puzzle 2: Nine Dots

Connect the all the dots without lifting your pen, using at most 4 straight lines, and without retracing any of the lines.

Answer To Puzzle 2: Nine Dots

Here is one way you can solve the puzzle. The trick is to think "outside the box."

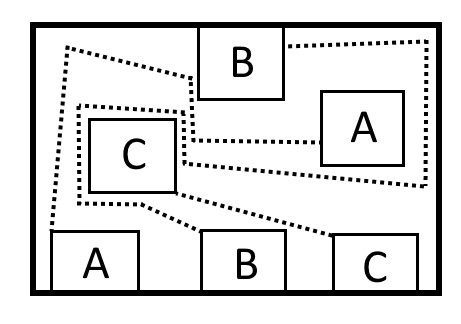
Puzzle 3: Six Boxes

Connect boxes of the same letter with lines. The lines cannot intersect and they have to stay inside of the boundary of the bordering box.

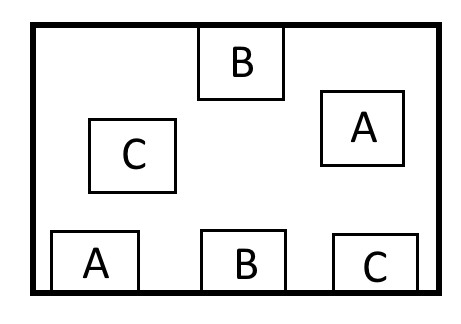
Answer To Puzzle 3: Six Boxes

Here is one way to solve the puzzle. To connect the two boxes with the letter B, wrap the line around the boxes for the letters A and C. Then there will be enough room to connect the remaining boxes without having to cross the path of any existing line.

Puzzle 4: Divide Into 4

Divide the following shape into 4 equal parts, where each part is the same shape and size.

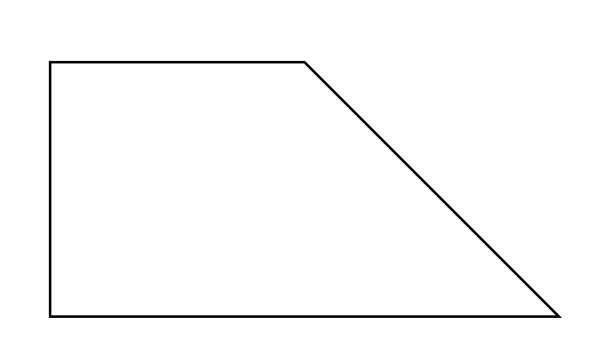
The dimensions are not listed because the figure is drawn to scale.

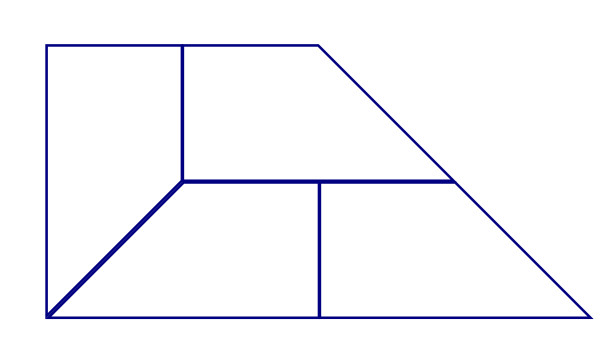
Answer To Puzzle 4: Divide Into 4

There's a neat trick to solve the puzzle: you can break the shape into 4 smaller copies of itself.

Puzzle 5: Circles In Triangles

Infinitely many circles are inscribed into an isosceles triangle with sides of 10, 13, and 13, as shown in the following diagram. What is the sum of the circumferences of all the circles?

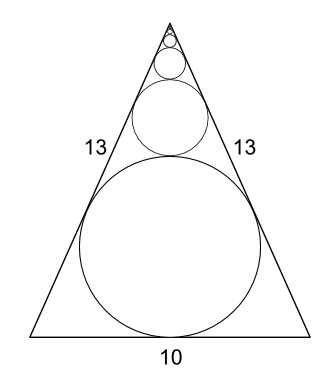
Answer To Puzzle 5: Circles In Triangles

You could solve for the circumference of each circle. An inscribed circle in a triangle has a radius equal to the area of the triangle divided by its semi-perimeter. In this problem, the largest circle has a radius of 60/18 = 10/3. By similar triangles, one could find out the ratio of each smaller circle. Skipping the details, each subsequent circle can be found to be 4/9 of the previous circle. The largest circumference is 2 r = (20/3) and each subsequent circumference is 4/9 of that. So we could solve the problem by summing the infinite geometric series starting with (20/3) and having a common ratio of 4/9.