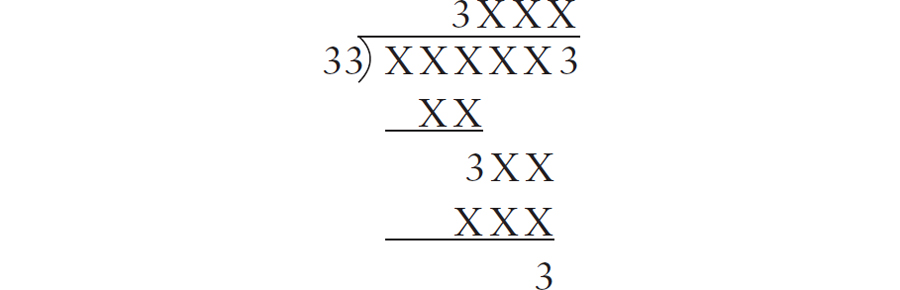Stickels - Challenging Math Problems.

Challenging Math Problems

TERRY STICKELS

DOVER PUBLICATIONS, INC.

Mineola, New York

Copyright

Copyright 2015 by Terry Stickels

All rights reserved.

Bibliographical Note

Challenging Math Problems is a new work, first published by

Dover Publications Inc., in 2015.

International Standard Book Number

eISBN-13-13: 978-0-486-80857-4

Manufactured in the United States by RR Donnelley

79553501 2015

www.doverpublications.com

INTRODUCTION

It is the wish of every writer to write that one book he/she has always wanted to see on book shelves. From what I have seen and read, it doesnt happen often. The book you now hold in your hands is that book for me. For over eight years, I put together the best and most challenging puzzles I could, hoping a good publisher would like it as much as I did. I kept them in a file and reviewed them weekly, often asking for advice and suggestions from some very bright people. When I had a discussion with Mr. John Grafton of Dover Publications about a possible book of puzzles, I was pleasantly surprised when he asked if I would be interested in doing a book of the most challenging puzzles imaginable. The puzzles had to be the kind that require no higher math ... just good thinking skills. And they had to be fun. They had to offer that AHA! moment of discovery that all puzzle solvers love. That was good for me because it is difficult to take myself or puzzles too seriously.

Regarding the aspect of having fun, I owe my outlook to the best puzzle writer, Martin Gardner. He got a kick out of everything he wrote about and puzzles were at the top of his list. During our discussions he would always mention some topic or puzzle that would make him laugh, followed by saying, I have never had to work a real job a day in my life. Ive been having fun my whole adult life. How many people can say that?!

So, if I have done my job properly, you will have a good time solving some demanding puzzles. Thats it. That is what I set out to do: keep things neat, straight-ahead, and fun. That is my reward for writing puzzles for a living.

ACKNOWLEDGMENTS

The following people have bent over backward for years helping me, often working weekends and nights just to make a puzzle perfect. Diana Smith is the editor for my Stickelers puzzle column syndicated by King Features. Her suggestions and keen eye catching my errors are invaluable. Terry Baughan is my graphic artist/designer for Stickelers and she takes painstaking efforts to make sure each graphic is the way I want it, a very difficult job. Christy Davis has been my associate for many years and is responsible for putting everything together. She is a wonderful puzzle writer, as well. Her Word Search puzzle books and calendars are great fun.

Special mention to two men who are both brilliant mathematicians and friends: Dr. John Konvalina, Department Chair of Mathematics at the University of Nebraska at Omaha and Dr. Harvy Baker of the Mathematics Department at the University of Texas Arlington. Both spent countless hours helping refine the puzzles in this book, making suggestions and explaining concepts in terms that I could, in turn, explain to the reader. They did this for the love of learning and for the fun of solving puzzles.

Thank you all.

Terry Stickels

www.terrystickels.com

PUZZLES

If a teacher can place his students eight to a bench, he will have only three students on the final bench. If he decides to place nine students on a bench, hell have only four students on the final bench. What is the smallest number of students this class could have?

Heres a probability puzzle that may test even some of the best mathematicians.

Imagine you have two opaque boxes. One box has one white marble and the other box has one white marble and one black marble. Of course, you cant see into either box. Simultaneously, you reach into both boxes, grab one marble from each, and quickly switch the marbles without looking at them. You then pick one of the marbles from one of the boxes. What is the probability the marble you pick is white?

Molly places 200 kilograms of watermelons in cases in front of her shop. At that moment, the watermelons are 99% water. In the afternoon, it turns out that it is the hottest day of the year, and as a result, the watermelons start to dry out. At the end of the day, Molly is surprised because she wasnt able to sell a single watermelon, and the melons are now only 98% water. How many kilograms of watermelons does Molly have left at the end of the day?

One of the most interesting studies in mathematics is the way numbers grow as they approach infinity. So, for this puzzle consider if you were to take the limit, as n approaches infinity, put the following in order, going from lowest to highest in value. Note: c is any positive integer you choose greater than 1. All values of n are positive and greater than one.

What number comes before the 3 to start this sequence?

? 3 11 31 75 155 283 471

A positive whole number is divisible by 3 and also by 5. When the number is divided by 7, the remainder is 5. What is the smallest number that could work?

What are the missing digits in the division below? All the 3s are given. The placeholder Xs may be any digit from 0 9, excluding 3.

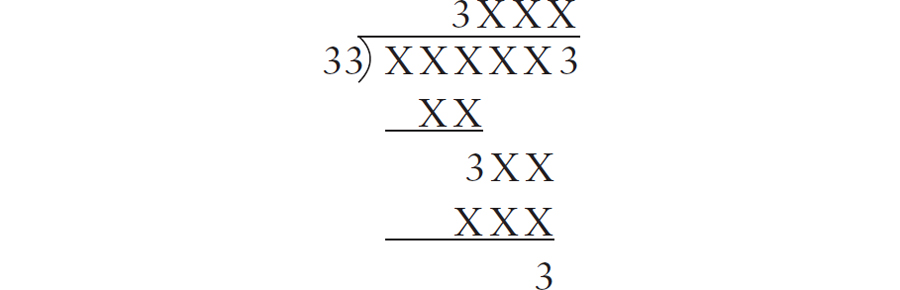
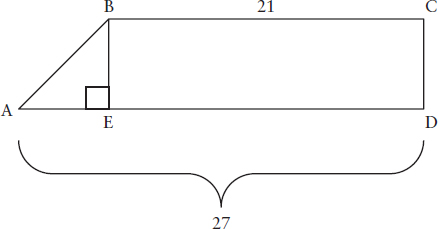
In the figure below, the total area of rectangle BCDE plus triangle ABE is 192 sq. units. What is the length of AB?

The mean of three numbers is 12 more than the least of the numbers and 18 less than the greatest. The median of the three numbers is 9. What is the sum of the three numbers?

Alison and Amelia live 14 miles apart. Alison started to drive her car toward Amelias house. At the same time, Amelia started to drive toward Alisons house. When they met, Alison had been driving for three times as long as Amelia and at 3/5 Amelias rate. How many miles had Amelia driven when they met?

On a normal die, the sum of the dots on opposite faces is seven.

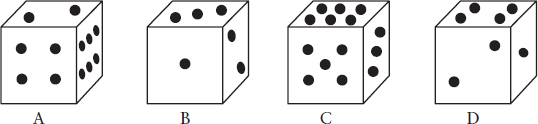
On the four dice above, the opposite faces total seven but one of the pictures is incorrect because of the orientation of the dots. Which die is incorrect? There is enough information from the four views to make this determination.

Below are 24 matchsticks arranged in a 3 3 grid. The circles represent the matchsticks that would have to be removed so that there are no squares of any size remaining in the grid. The minimum number, as you can see, is six matchsticks that need to be removed. There are several ways to accomplish this.

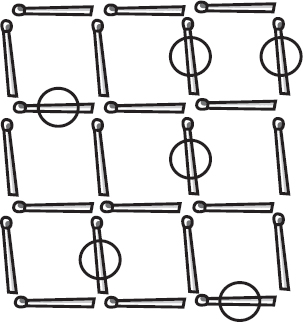
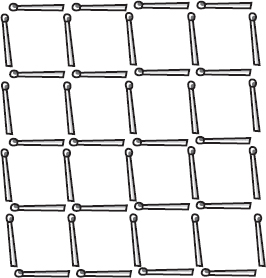
Now, what is the minimum number of matchsticks that need to be removed in a 4 4 grid of 40 matchsticks? Remember, there can be no squares, of any size, remaining.

For what value K is the following system consistent?