Paul J. Nahin - Will You Be Alive 10 Years from Now?: And Numerous Other Curious Questions in Probability

Will You Be Alive

10 Years from Now?

Will You Be Alive

10 Years from Now?

And Numerous Other Curious

Questions in Probability

A collection of not so well-known mathematical mind-benders
(with solutions, with one exception)

PAUL J. NAHIN

PRINCETON UNIVERSITY PRESS

PRINCETON AND OXFORD

Copyright 2014 by Princeton University Press
Published by Princeton University Press, 41 William Street,
Princeton, New Jersey 08540
In the United Kingdom: Princeton University Press,
6 Oxford Street, Woodstock, Oxfordshire OX20 1TW

press.princeton.edu

Jacket art by Dimitri Karetnikov

All Rights Reserved

Library of Congress Cataloging-in-Publication Data

Nahin, Paul J.
Will you be alive 10 years from now? : and numerous other curious questions in probability : a collection of not so well-known mathematical mind-benders (with solutions, with one exception) / Paul J. Nahin.
pages cm

Summary: What are the chances of a game-show contestant finding a chicken in a box? Is the Hanukkah dreidel a fair game? Will you be alive ten years from now? These are just some of the one-of-a-kind probability puzzles that acclaimed popular math writer Paul Nahin offers in this lively and informative book. Nahin brings probability to life with colorful and amusing historical anecdotes as well as an electrifying approach to solving puzzles that illustrates many of the techniques that mathematicians and scientists use to grapple with probability. He looks at classic puzzles from the pastfrom Galileos dice-tossing problem to a disarming dice puzzle that would have astonished even Newtonand also includes a dozen challenge problems for you to tackle yourself, with complete solutions provided in the back of the book. Nahin then presents twenty-five unusual probability puzzlers that you arent likely to find anywhere else, and which range in difficulty from ones that are easy but clever to others that are technically intricate. Each problem is accompanied by an entertaining discussion of its background and solution, and is backed up by theory and computer simulations whenever possible in order to show how theory and computer experimentation can often work together on probability questions. All the MATLAB Monte Carlo simulation codes needed to solve the problems computationally are included in the book. With his characteristic wit, audacity, and insight, Nahin demonstrates why seemingly simple probability problems can stump even the experts.Provided by publisher.

Includes bibliographical references and index.

ISBN 978-0-691-15680-4 (hardback)

1. ProbabilitiesProblems, exercises, etc. I. Title.

QA273.25.N344 2014

519.2dc23 2013010221

British Library Cataloging-in-Publication Data is available

This book has been composed in ITC New Baskerville

Printed on acid-free paper.

Printed in the United States of America

1 3 5 7 9 10 8 6 4 2

For Patricia Ann

who, after fifty years of marriage, can still surprise me

even more than a good probability problem can!

If we do everything right, if we do it with absolute certainty, theres still a 30 percent chance were going to get it wrong.

Joseph R. Biden, vice president of the United States, during a 2009 political talk in Williamsburg, Virginia, that showed a shaky understanding of probability is no roadblock to higher elective office in America

What has hit Los Angeles is a force of nature that is exactly the same as a flood or a fire or an earthquake. Its the natural law of probability. Given four to five million vehicles traveling on those freeways each day, a certain number of accidents will happen. It was mathematically unlikely that one would happen at each of seventeen major interchanges simultaneously on any given day, but the odds caught up with us. Mathematics is a force of nature, too.

From Thomas Perrys very funny 1983 novel Metzgers Dog, in which LA thieves show that the CIAs middle initial might be claiming just a bit too much

There are few persons, even among the calmest thinkers, who have not occasionally been startled into a vague yet thrilling half-credence in the supernatural, by coincidences of so seemingly marvelous a character that, as mere coincidences, the intellect has been unable to receive them. Such sentiments are seldom thoroughly stifled unless by reference to the doctrine of chance, or as it is technically termed, the Calculus of Probabilities. Now this Calculus is, in its essence, purely mathematical; and thus we have the anomaly of the most rigidly exact in science applied to the shadow and spirituality of the most intangible in speculation.

The opening words of Edgar Allen Poes
The Mystery of Marie Rogt (1842/3)

Contents

Preface

P robability problems fascinate just about everyone, despite wildly varying backgrounds that span the sophistication spectrum. Mathematicians love them because probability theory is so beautiful, one of the gems of mathematics. Physicists love them because probability often is the key to answering many of their technical questions. And everybody loves probability problems simply because they can be a lot of fun. A probability problem can simultaneously be so easy to state that anybody with a brain can understand the question, while also being so puzzling that even the experts are stumped (at least for a while).

Heres an example of what I mean by that. Suppose we have an urn with 100 red balls and 100 black balls in it. Suppose further that we select balls, one after the other, with replacementthat is, after selecting a ball we put it back in the urn. Then,

(a) Whats the probability the first ball is red? The answer is, of course, 1/2.

(b) Whats the probability the second ball is red? Ho, hum, you say, its 1/2, too, of course!

Now, suppose we select balls without replacement, that is, after drawing a ball we discard it. Then,

(c) Whats the probability the first ball is red? My gosh, you say, this is getting boringits clearly still 1/2 because it doesnt matter what we do with first ball after we select it.

(d) Whats the probability the second ball is red? Okay, you shout, at last a nonobvious question! Now, you surely say, the answer depends on what the first ball was because if the first ball was red, then there would be just 99 red balls in the urn for the second drawing, while if the first ball was black, then there would still be 100 red balls available but only 99 black balls.

This does seem to be more complicated than were the earlier cases. What we can write is the following, using what are called conditional probabilities:

Prob(second ball is red) = Prob(second ball is red given that the first ball is red) Prob(first ball is red) + Prob(second ball is red given that the first ball is black) Prob(first ball is black)

= (99/199)(100/200) + (100/199)(100/200) = (100/200)(99/199 + 100/199) = (100/200)(199/199) = .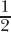

Now, if this result doesnt surprise youits still 1/2well, all I can say is that I used this example in my classes for decades, and it still makes me scratch my head!

Or how about this amazing result. Each of a million men puts his hat into a very large box. Every hat has its owners name on it. The box is given a good shaking, and then each man, one after the other, randomly draws a hat out of the box. Whats the probability that at least one of the men gets his own hat back? Most people would answer with pretty slim, but in fact the answer is the astonishingly large 0.632! Who would have guessed that?