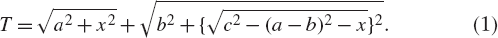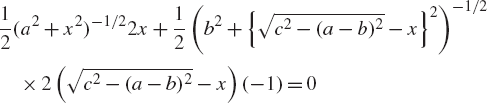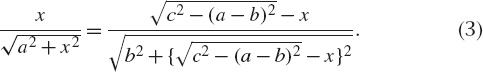Paul J. Nahin - When Least Is Best: How Mathematicians Discovered Many Clever Ways to Make Things as Small (or as Large) as Possible

Copyright 2004 by Princeton University Press

Preface to the new paperback edition,
copyright 2021 by Princeton University Press

Published by Princeton University Press,
41 William Street, Princeton, New Jersey 08540

In the United Kingdom: Princeton University Press,
6 Oxford Street, Woodstock, Oxfordshire OX20 1TR

All Rights Reserved

First published by Princeton University Press in 2004

First paperback, 2007

First Princeton Science Library paperback edition, 2021

Paperback ISBN 978-0-691-21876-2

Library of Congress Control Number: 2020949714

British Library Cataloging-in-Publication Data is available

This book has been composed in Stone

press.princeton.edu

Printed in the United States of America

For PATRICIA ANN ,

who contradicts the title because she has always been

the most and is still the best

When a quantity is the greatest or the least that it can be, at that moment it neither flows backwards nor forwards; for if it flows forwards or increases it was less, and will presently be greater than it is; and on the contrary if it flows backwards or decreases, then it was greater, and will presently be less than it is.

Isaac Newton on maximums and minimums, in Methodus fluxionum et serierum infinitarum, 1671

There are hardly any speculations in geometry more useful or more entertaining than those which relate to maxima and minima.

the great English mathematician Colin Maclaurin, in A Treatise of Fluxions, 1742

The great body ofphysical science, a great deal of the essential fact of financial science, and endless social and political problems are only accessible and only thinkable to those who have had a sound training in mathematical analysis, and the time may not be very remote when it will be understood that for complete initiation as an efficient citizen of one of the great complex world-wide States that are now developing, it is as necessary to be able to compute, to think in averages and maxima and minima, as it is now to be able to read and write.

H. G. Wells, from Mankind in the Making, 1903

T he selection of When Least Is Best, first published in 2004, for inclusion in the Princeton Science Library was a wonderful surprise for me (and thats a vast understatement), joining two of my other math books (An Imaginary Tale and Dr. Eulers Fabulous Formula). That event provided me with the until-now-only-dreamed-of chance to eliminate some awkward missteps that somehow slipped through while preparing the earlier editions of the book. On the flip side, the books reissue also provided me with the opportunity to present one more problem discussion, a problem I have long wished I had included in the original work. I have berated myself for years in having overlooked this particular problem, with its many educational features. It is, in particular, a minimization problem that (1) is understandable in its goal by even a grammar school student; (2) is well within the mathematical reach of a high school AP calculus student; (3) and yet, despite (2), is analytically pretty nasty unless one is just a bit clever and sees a trick that foreshadows one of the great principles of classical physics, a trick that neatly sidesteps the nastiness; and finally (4) is a practical, realistic problem that almost surely has, more than just a few times, actually occurred in real life. So, with that big buildup, here it is.

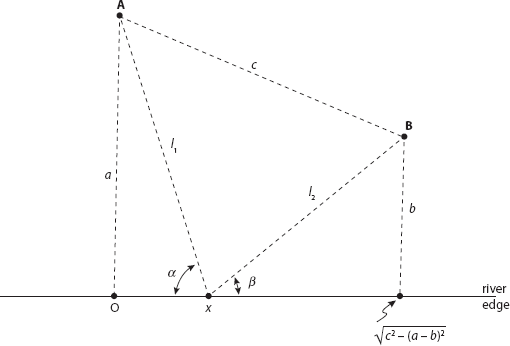
Two towns, A and B, are located on the same side of a straight river. The distance of A from the river is a, and the distance of B from the river is b. The distance between A and B is c. The towns enter into an agreement to jointly construct a water filtration and pumping station on the rivers edge and to directly connect that facility to each town with two pipelines, one of length l1 to A and another of length l2 to B. The total length of pipeline required obviously depends on where the facility is constructed, with the optimum choice for the location being that which minimizes l1 + l2. What (in terms of a, b, and c) is that minimum value? The geometry of this problem is shown in Figure 1, where, with no loss of generality, we take ab.

FIGURE 1. The geometry of the water filtration/pumping station problem.

In Figure 1 the point on the river edge that is directly below A is assigned the coordinate of zero, and the facility is assigned coordinate x (which is, of courseat least for nowunknown). The point on the river edge that is directly below B has coordinate , an expression that follows from an obvious application of the Pythagorean theorem. The angles and that the pipelines make with the rivers edge may not have immediately obvious significance but, as youll soon see, they will be key to answering our question.

If we write T = l1 + l2 then

Our problem is to find the x that minimizes T and, as we know from AP calculus, that suggests our next step is to study the equation

The vanishing of the first derivative does not ensure the existence of an extrema (like a local minimum), of course, but the geometry of the problem does make it highly plausible, by inspection of Figure 1, that a minimum of T does exist for some x between 0 and . If so, then expression (2) will hold there, and in the following analysis we will establish that a minimum does, in fact, exist.

So, returning to expression (2), we would like to solve

for x. Or, after a little bit of obvious simplification, we want to solve

Well, we might want to solve expression (3) for x, but to that all I can say is: lots of luck! And even if you manage to do that, you then have to plug that value of