Frontispiece CALVIN AND HOBBES 1988 Patterson. Distributed by UNIVERSAL PRESS SYNDICATE. Reprinted with permission. All rights reserved.
Preface to the Paperback Edition
THE HARDCOVER EDITION of this book appeared in 1998, and for the eight long years since, I have had to go to bed every single night thinking about dumb typos, stupid missing minus signs, and embarrassingly awkward phrases. Each has been like a sliver of wood under a fingernail. None of them was life threatening, of course, but together they made my intellectual life less than perfect. For the first six months after the book first came out I'd wake up at night, muttering to myself much as the eccentric Victorian electrical physicist Oliver Heaviside had done when he was approaching his sixties: I must be getting as stupid as an owl. Those were interesting timesthe life of the elderly mathematics writer can be a stressful one.
But no more! Over the years readers have generously taken the time to send me their discoveries of my oversights, and with their lists in one hand and a red pen in the other, I have joyfully pulled those irritants out of this paperback edition. Probably not all of them, alas, but still, I do feel better (a feeling that will no doubt vanish upon receiving the next e-mail or letter telling me of one or more errors I have missed). Two long, detailed letters I received in 1999 from Professors Robert Burckel (Dept. of Mathematics, Kansas State University) and David Wunsch (Dept. of Electrical Engineering, University of Massachusetts at Lowell) were particularly helpful. Princeton University Press published the sequel to this book, Doctor Euler's Fabulous Formula, earlier this year, and so the appearance so soon after of a corrected and updated edition of An Imaginary Tale is particularly gratifying. I thank my editor at Princeton, Vickie Kearn, for providing me this opportunity to revisit the book. Now, on to what's changed in this edition besides corrected misprints.
Actually, and perhaps somewhat inconsistently, I'll start by mentioning some things that haven't changed. While I carefully read everything that readers sent me, and while I admit that the vast majority of what was sent to me ended up having a significant impact on the corrections to the book, there were a few exceptions. Let me give you just two examples of this. To start, one reader took me to task rather severely for declaring (on p. 9) that del Ferro's breakthrough idea that cracked the depressed cubic equation was of the magician class. No, no, no, said the reader (who claimed he was a professional mathematician), that was merely a good idea that lots of people could have had. Well, to that I can only say that nobody before del Ferro did have that idea. Whatever might be asserted about what mathematicians might have done, or could have done, or even should have done in the past, the fact remains that it was del Ferro who solved the depressed cubic. I think my sophisticated critical reader has just forgotten how much he himself must have been impressed when he first saw how to solve a cubic equation.
Familiarity breeds contempt is a clich precisely because it is true. As an example of what I'm getting at here, every good high-school math student today knows how to prove 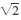 is irrational, but that doesn't mean it's now just a ho-hum demonstration. Twenty-five centuries or so ago the discovery of irrational numbers was a revolutionary event in mathematics, and good students still oooh and aaah when they first see the proof for
is irrational, but that doesn't mean it's now just a ho-hum demonstration. Twenty-five centuries or so ago the discovery of irrational numbers was a revolutionary event in mathematics, and good students still oooh and aaah when they first see the proof for 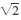 . In the same way, I think my critical reader is dead wrong about the depressed cubic, and so I have not changed a single word in the book's discussion of del Ferro.
. In the same way, I think my critical reader is dead wrong about the depressed cubic, and so I have not changed a single word in the book's discussion of del Ferro.
As a second example of an error that wasn't, a reader wrote to complain that in (the circuit diagram of a phase-shift oscillator) the voltage u is to the right of voltage v, but in the text I refer to the voltage













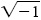 has long labored under a similar false story of unfathomable mystery. The French philosophical genius of the Enlightenment, Denis Diderot, wrote of mathematicians that they resemble those who gaze out from the tops of high mountains whose summits are lost in the clouds. Objects on the plain below have disappeared from view; they are left with only the spectacle of their own thoughts and the consciousness of the height to which they have risen and where perhaps it is not possible for everyone to follow and breathe [the thin air]. Well, in this book the air is almost always at sea-level pressure. Large chunks of this book can, in fact, be read and understood by a high school senior who has paid attention to his or her teachers in the standard fare of precollege courses. Still, it will be most accessible to the million or so who each year complete a college course in freshman calculus. It is not a textbook, but I do think it could be profitably read by students as a supplement to the more standard presentations of mathematics. I am an electrical engineer, not a mathematician, and the style of the writing reflects the difference. Indeed, I have taken advantage of my freedom from the usual dictates of textbook pedagogywhich in its worst form can be pedanticto write in a casual and, I hope, entertaining style. But when I need to do an integral, let me assure you I have not fallen to my knees in dumbstruck horror. And neither should you. The power and beauty of complex numbers and functions, and the amazing story of their discovery, will amply repay any extension of concentration that the relatively harder parts may demand.
has long labored under a similar false story of unfathomable mystery. The French philosophical genius of the Enlightenment, Denis Diderot, wrote of mathematicians that they resemble those who gaze out from the tops of high mountains whose summits are lost in the clouds. Objects on the plain below have disappeared from view; they are left with only the spectacle of their own thoughts and the consciousness of the height to which they have risen and where perhaps it is not possible for everyone to follow and breathe [the thin air]. Well, in this book the air is almost always at sea-level pressure. Large chunks of this book can, in fact, be read and understood by a high school senior who has paid attention to his or her teachers in the standard fare of precollege courses. Still, it will be most accessible to the million or so who each year complete a college course in freshman calculus. It is not a textbook, but I do think it could be profitably read by students as a supplement to the more standard presentations of mathematics. I am an electrical engineer, not a mathematician, and the style of the writing reflects the difference. Indeed, I have taken advantage of my freedom from the usual dictates of textbook pedagogywhich in its worst form can be pedanticto write in a casual and, I hope, entertaining style. But when I need to do an integral, let me assure you I have not fallen to my knees in dumbstruck horror. And neither should you. The power and beauty of complex numbers and functions, and the amazing story of their discovery, will amply repay any extension of concentration that the relatively harder parts may demand.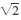 is irrational, but that doesn't mean it's now just a ho-hum demonstration. Twenty-five centuries or so ago the discovery of irrational numbers was a revolutionary event in mathematics, and good students still oooh and aaah when they first see the proof for
is irrational, but that doesn't mean it's now just a ho-hum demonstration. Twenty-five centuries or so ago the discovery of irrational numbers was a revolutionary event in mathematics, and good students still oooh and aaah when they first see the proof for