PENGUIN BOOKS
IMAGINING NUMBERS
Barry Mazur is a celebrated pure mathematician. He is the Gerhard Gade University Professor at Harvard. His work has been influential in many fields and was important for Wiles's proof of Fermat's Last Theorem.
IMAGINING NUMBERS
(particularly the square root of minus fifteen)
BARRY MAZUR
PENGUIN BOOKS
PENGUIN BOOKS
Published by the Penguin Group
Penguin Books Ltd, 80 Strand, London WC2R 0RL, England
Penguin Group (USA) Inc., 375 Hudson Street, New York, New York 10014, USA
Penguin Books Australia Ltd, 250 Camberwell Road, Camberwell, Victoria 3124, Australia
Penguin Books Canada Ltd, 10 Alcorn Avenue, Toronto, Ontario, Canada M4V 3B2
Penguin Books India (P) Ltd, 11 Community Centre, Panchsheel Park, New Delhi 110 017, India
Penguin Books (NZ) Ltd, Cnr Rosedale and Airborne Roads, Albany, Auckland, New Zealand
Penguin Books (South Africa) (Pty) Ltd, 24 Sturdee Avenue, Rosebank 2196, South Africa
Penguin Books Ltd, Registered Offices: 80 Strand, London WC2R 0RL, England
www.penguin.com
First published in the USA by Farrar, Straus and Giroux 2003
First published in Great Britain by Allen Lane 2003
Published in Penguin Books 2004
Copyright Barry Mazur, 2003
All rights reserved
The moral right of the author has been asserted
Grateful acknowledgment is made for use of the following illustrations:
Except in the United States of America, this book is sold subject to the condition that it shall not, by way of trade or otherwise, be lent re-sold, hired out, or otherwise circulated without the publisher's prior consent in any form of binding or cover other than that in which it is published and without a similar condition including this condition being imposed on the subsequent purchaser
ISBN: 978-0-14-193170-8
To Gretchen
CONTENTS
PREFACE
1, 2, 3, The counting numbers are part of us. We know them forward and backward. Babies as young as five months old, psychologists claim, are sensitive to the difference between 1 + 1 and 2 1. We sing numbers, counting up the days of Christmas and counting down to the poignant monotheism of One is one and all alone and evermore shall be so.
Our ancestors have added to this repertoire and reckoned with zero and the negative numbers, which were sometimes referred to as fictions (fictae) before they gained familiarity.
All these together constitute what we call the whole numbers,
, 2, 1, 0, +1, +2,
More formally, they are called integers, from the Latin adjective meaning whole, untouched, unharmed.
Whole, untouched; their very name hints that integers can be touched, or fractionated. Indeed they can be, and when they are, we get the larger array of numbers that are fractions, ratios of whole numbers.
Fractions, as their notation vividly displays, also stand for proportions (think of 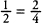 as one is to two as two is to four) and for actions (think of
as one is to two as two is to four) and for actions (think of 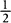 as halving, ready to cut in half anything that follows it).
as halving, ready to cut in half anything that follows it).
To bring fractions into line, we express them as decimals 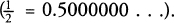 The modern world gives us much experience with decimals to a high degree of accuracyto many decimal places; mathematics, as always, goes all the way, happy to deal with numbers with complete accuracyto infinitely many decimal places. Numbers represented by infinitely many decimal places, whether they are fractions or not, are called real numbers.
The modern world gives us much experience with decimals to a high degree of accuracyto many decimal places; mathematics, as always, goes all the way, happy to deal with numbers with complete accuracyto infinitely many decimal places. Numbers represented by infinitely many decimal places, whether they are fractions or not, are called real numbers.
But the telltale adjective real suggests two things: that these numbers are somehow real to us and that, in contrast, there are unreal numbers in the offing. These are the imaginary numbers.
The imaginary numbers are well named, for there is some imaginative work to do to make them as much a part of us as the real numbers we use all the time to measure for bookshelves.
This book began as a letter to my friend Michel Chaouli. The two of us had been musing about Michel had also mentioned that he wanted to imagine imaginary numbers. That very (rainy) evening, I tried to work up an explanation of the idea of these numbers, still in the mood of our conversation.
The text of my letter was the welcome excuse for continued conversation with a number of friends, many of whom were humanists interested in understanding what it means to imagine the square root of negative numbers. The successive revisions and expansions of my letter were shaped by their questions, comments, critiques, and insights. This book, then, is written for people who have no training in mathematics and who may not have actively thought about mathematics since high school, or even during it, but who may wish to experience an act of mathematical imagining and to consider how such an experience compares with the imaginative work involved in reading and understanding a phrase in a poem. Of course, poetry and mathematics are far apart. All the more glorious, then, for people at home in the imaginative life of poetry to use their insight and sensibility to witness the imagination at work in mathematics.
Although no particular mathematical knowledge is necessary, pencil and paper are good to have at hand, to make a few calculations (multiplying small numbers, mostly). The operation of multiplication itself is something we will be looking at. There are three standard ways of denoting the act of multiplication: by a cross X, by a centered dot., or, when there is no ambiguity, by simple juxtaposition of the objects to be multiplied. Which notation we use reflects where we wish to direct our attention: the equation
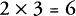
emphasizes the act of multiplying 2 times 3, whereas
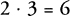
focuses on the result, 6, of that operation. Nevertheless, despite this difference in nuance, both equations, 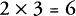 and
and 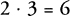 , are saying the same thing. When we deal with an unknown quantity X, here are three equivalent ways of denoting 5 times that unknown quantity:
, are saying the same thing. When we deal with an unknown quantity X, here are three equivalent ways of denoting 5 times that unknown quantity:
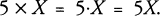
Again, we write 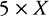 if we want to emphasize the act of multiplying and
if we want to emphasize the act of multiplying and 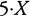 or
or 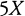 if we want to emphasize the result; and that last variant notation, juxtaposition, is used for visual conciseness.
if we want to emphasize the result; and that last variant notation, juxtaposition, is used for visual conciseness.
This book has footnotes and endnotes. Some of the endnotes are side comments requiring more mathematical background than is assumed in the text.
Next page










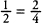 as one is to two as two is to four) and for actions (think of
as one is to two as two is to four) and for actions (think of 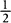 as halving, ready to cut in half anything that follows it).
as halving, ready to cut in half anything that follows it).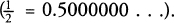 The modern world gives us much experience with decimals to a high degree of accuracyto many decimal places; mathematics, as always, goes all the way, happy to deal with numbers with complete accuracyto infinitely many decimal places. Numbers represented by infinitely many decimal places, whether they are fractions or not, are called real numbers.
The modern world gives us much experience with decimals to a high degree of accuracyto many decimal places; mathematics, as always, goes all the way, happy to deal with numbers with complete accuracyto infinitely many decimal places. Numbers represented by infinitely many decimal places, whether they are fractions or not, are called real numbers.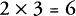
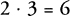
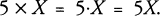
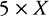 if we want to emphasize the act of multiplying and
if we want to emphasize the act of multiplying and 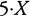 or
or 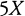 if we want to emphasize the result; and that last variant notation, juxtaposition, is used for visual conciseness.
if we want to emphasize the result; and that last variant notation, juxtaposition, is used for visual conciseness.