CONTEMPORARYBRAINTEASERSCONTEMPORARYBRAINTEASERSTERRY STICKELSDOVER PUBLICATIONS, INC.MINEOLA, NEW YORKCopyright Copyright 2016 by Terry Stickels All rights reserved. Bibliographical NoteContemporary Brainteasers is a new work, first published by
Dover Publications Inc., in 2016. International Standard Book NumberISBN-13: 978-0-486-80782-9ISBN-10: 0-486-80782-7 Manufactured in the United States by LSC Communications 80782701 2016 www.doverpublications.com CONTENTSINTRODUCTION I have read numerous articles on how puzzles are good exercise for the mind, how they augment critical thinking skills, and even how they can help in preventing or delaying dementia in some people. To date, I have not seen any scientific studies backing these positions. Of course, it would be to my advantage if this were otherwise. But there is a definite positive side to this.
Without question, the better math puzzles offer the solver some interesting perspectives on how to solve problems. Puzzles are not bound by the same rigorous rules and algorithms of academic mathematics. Because of this, there is more wiggle room on how to reach a solution. In other words, solve the puzzle any way you can we dont need to see your work to give you credit. But the mere fact that you are seeing solutions that you would never see in a classroom is a bonus in how you might approach other problems. Without any hard evidence, I make the claim that these types of puzzles have the ability to increase your mental flexibility.
If you do enough of them, you will start to view other problems from different perspectives. Unfortunately, my position is anecdotal. There is no study confirming this. But if the views of my readers over the years are any indication, there is something to this and it stands to reason. If you show me five different ways to fix something or solve a problem, I am going to consider alternative approaches in other situations if I get stumped again. The nice thing about puzzles is that they are for fun.
No one is grading you or writing a job performance review. Kick back and try your skill at solving a few of these puzzles. Its in your blood. You are the direct result of many successful solutions made prior to your being here. Push those limits. We dont think anything about asking our young athletes to push their limits physically.
Doesnt it make good sense that pushing the limits of your gray matter might have significant benefits? The puzzles you now hold in your hands will push the limits of even the best puzzle solvers. But take that as a challenge to confront. Make these puzzles fun and see how good it feels when you solve one. (They are even more fun to create.) In any event, dont take yourself too seriously while solving these. Remember, challenging fun is all I ever intended. PUZZLES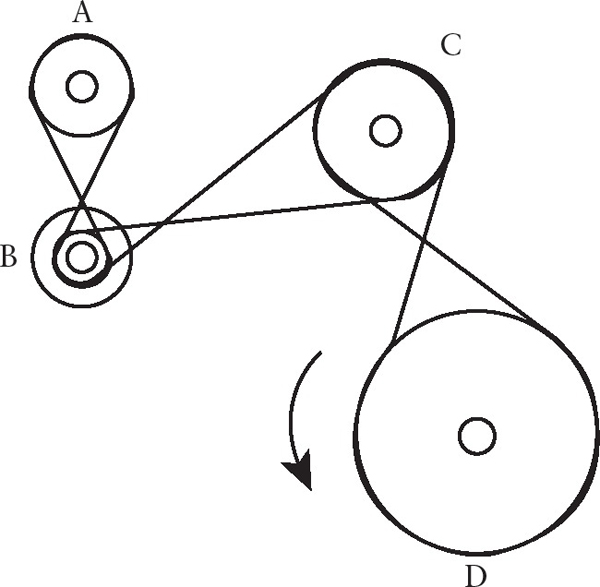 If pulley D is rotating in the direction of the arrow, then pulley A (a) is moving in the same direction (b) is moving in the opposite direction (c) will not be able to move at all.
If pulley D is rotating in the direction of the arrow, then pulley A (a) is moving in the same direction (b) is moving in the opposite direction (c) will not be able to move at all.
How many cubes of any size are contained in this stack? All rows and columns run to completion unless you actually see them end. 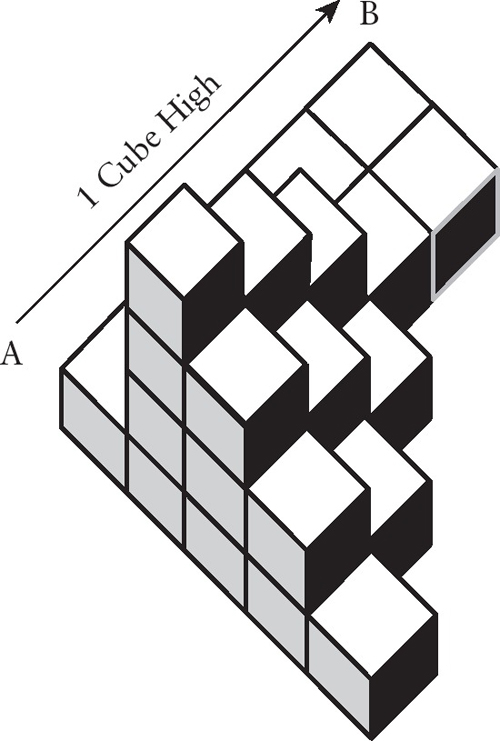 A bucket filled with water weighs 25 lbs. When one-half of the water is poured out, the bucket and remaining water weigh 13.5 lbs. How much does the bucket weigh? The three sides of a triangle have prime number lengths, w, x, and y, where 10<w<x<y<40. If x = 19, how many possible perimeters does this triangle have? (a) 5 (b) 8 (c) 13 (d) 21 (e) infinite With a normal deck of 52 playing cards, on what card dealt is the probability of getting a straight (five consecutive cards of any suit) 100%? In other words, how many cards would I have to deal to you, face down, before you tell me to stop because you know, with 100% accuracy, you have a straight? If it were three hours later it would be half as long until midnight as it would be if it were one hour earlier. What time is it now? If 1/3 = 7 in some other system, then 5/16 is equal to what in that system? Each figure contained within the largest square is also a square.
A bucket filled with water weighs 25 lbs. When one-half of the water is poured out, the bucket and remaining water weigh 13.5 lbs. How much does the bucket weigh? The three sides of a triangle have prime number lengths, w, x, and y, where 10<w<x<y<40. If x = 19, how many possible perimeters does this triangle have? (a) 5 (b) 8 (c) 13 (d) 21 (e) infinite With a normal deck of 52 playing cards, on what card dealt is the probability of getting a straight (five consecutive cards of any suit) 100%? In other words, how many cards would I have to deal to you, face down, before you tell me to stop because you know, with 100% accuracy, you have a straight? If it were three hours later it would be half as long until midnight as it would be if it were one hour earlier. What time is it now? If 1/3 = 7 in some other system, then 5/16 is equal to what in that system? Each figure contained within the largest square is also a square.
What are the sizes of the squares with the question marks? 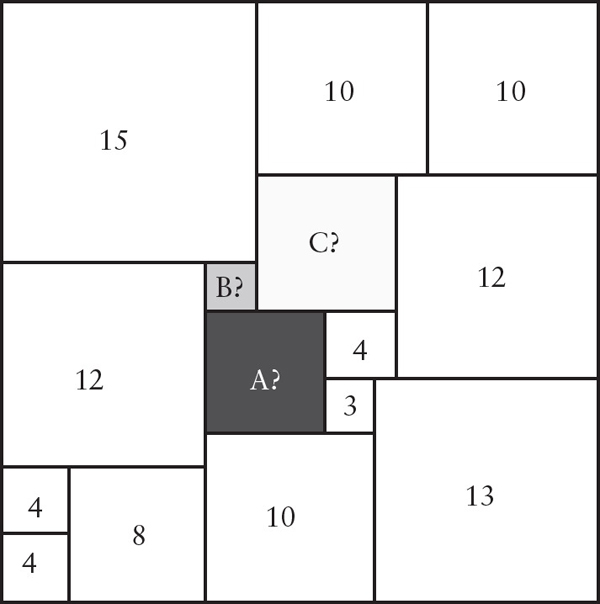 If the figure below is folded back into a cube, what side is opposite the blackened square? What about opposite the transparent circle?
If the figure below is folded back into a cube, what side is opposite the blackened square? What about opposite the transparent circle? 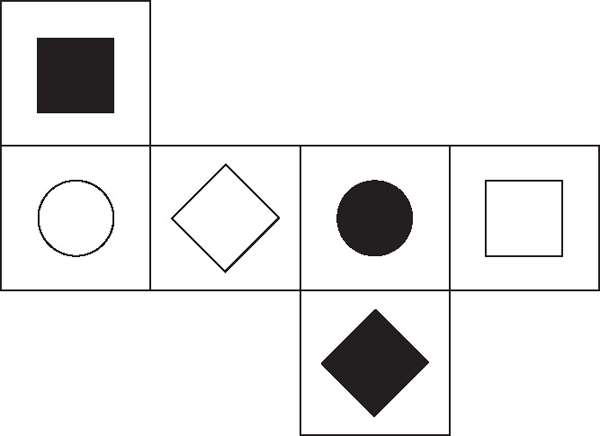
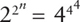 A solution for n is (a) 4 (b) 9 (c) 64 (d) 128 (e) 256 Here is a coin puzzle that may appear to have a counterintuitive answer, but I assure you it is correct. I flip a penny and a dime and hide the results from you but tell you at least one of the coins came up heads. What is the probability that both coins came up heads? The letters A U V T Y have reflection symmetry across a vertical plane. The letters H I O X have both horizontal and vertical symmetry. What capital letters have reflection symmetry across the horizontal plane only? If 10! (10 9 8 7 6 5 4 3 2 1) were to be factored into prime numbers, how many 5 s would appear? What if the number were 15!, how many 5s then?
A solution for n is (a) 4 (b) 9 (c) 64 (d) 128 (e) 256 Here is a coin puzzle that may appear to have a counterintuitive answer, but I assure you it is correct. I flip a penny and a dime and hide the results from you but tell you at least one of the coins came up heads. What is the probability that both coins came up heads? The letters A U V T Y have reflection symmetry across a vertical plane. The letters H I O X have both horizontal and vertical symmetry. What capital letters have reflection symmetry across the horizontal plane only? If 10! (10 9 8 7 6 5 4 3 2 1) were to be factored into prime numbers, how many 5 s would appear? What if the number were 15!, how many 5s then? 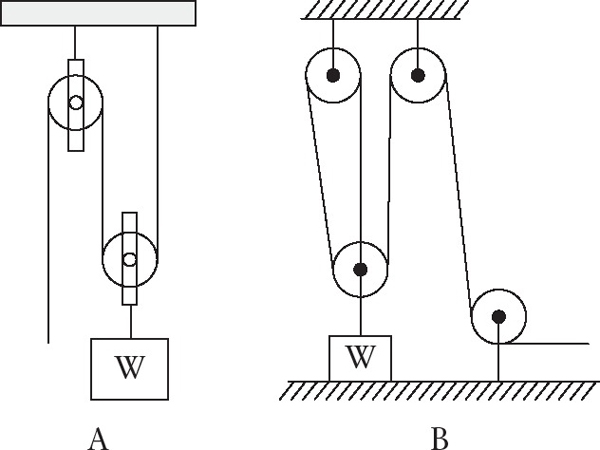 In the pulley system above: (a) A has a mechanical advantage of 2 and
In the pulley system above: (a) A has a mechanical advantage of 2 and
B has a mechanical advantage of 3. (c) A has a mechanical advantage of 2 and B has a mechanical advantage of 4. (d) Both systems have a mechanical advantage of 2. (e) Both systems have a mechanical advantage of 3. (e) Both systems have a mechanical advantage of 3.
Which choice is the correct one? 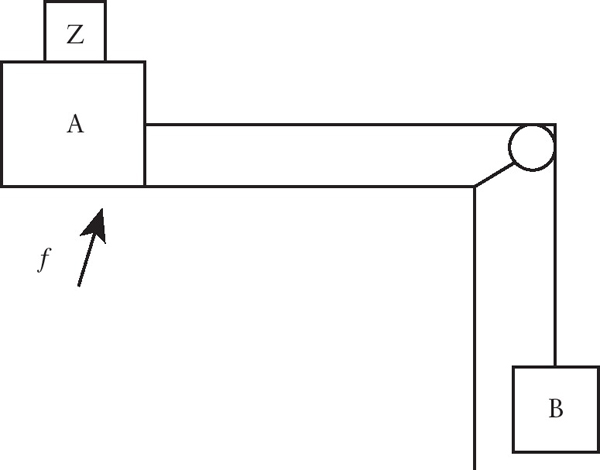 In the picture, the weight of A is 20, the weight of B is 10, and the coefficient of friction f is .2 How heavy must Z be to keep A from sliding? At a recent small gathering of friends, there were nine more women than men. If the ratio of women to men was 5 to 2, how many men and women were at the party? I have a few objects I need to weigh with weights from 1 to 40 ounces. What are four weights I can use to be able to weigh any weight from 1 to 40 ounces (whole number weights only and including 1 and 40 ounces)? Im trying to keep the number of weights I buy to a minimum, so what is the least number I would have to purchase of each of these four weights to accomplish my goal? What number comes next? Remember, anything goes with sequence puzzles. 33 20 14 11 In the formula below, what is the value of g? v = f (1g)t Given five points in space, connecting three points at a time to determine a plane (extending to infinity) what is the maximum number of lines that will result from all intersections? Each figure contained within the largest square is also a square. What are the sizes of squares A, B, C, and D?
In the picture, the weight of A is 20, the weight of B is 10, and the coefficient of friction f is .2 How heavy must Z be to keep A from sliding? At a recent small gathering of friends, there were nine more women than men. If the ratio of women to men was 5 to 2, how many men and women were at the party? I have a few objects I need to weigh with weights from 1 to 40 ounces. What are four weights I can use to be able to weigh any weight from 1 to 40 ounces (whole number weights only and including 1 and 40 ounces)? Im trying to keep the number of weights I buy to a minimum, so what is the least number I would have to purchase of each of these four weights to accomplish my goal? What number comes next? Remember, anything goes with sequence puzzles. 33 20 14 11 In the formula below, what is the value of g? v = f (1g)t Given five points in space, connecting three points at a time to determine a plane (extending to infinity) what is the maximum number of lines that will result from all intersections? Each figure contained within the largest square is also a square. What are the sizes of squares A, B, C, and D? 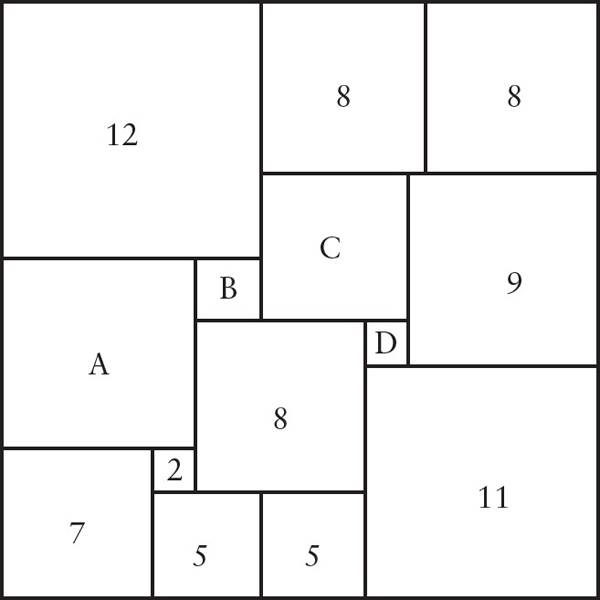
Next page








 If pulley D is rotating in the direction of the arrow, then pulley A (a) is moving in the same direction (b) is moving in the opposite direction (c) will not be able to move at all.
If pulley D is rotating in the direction of the arrow, then pulley A (a) is moving in the same direction (b) is moving in the opposite direction (c) will not be able to move at all. A bucket filled with water weighs 25 lbs. When one-half of the water is poured out, the bucket and remaining water weigh 13.5 lbs. How much does the bucket weigh? The three sides of a triangle have prime number lengths, w, x, and y, where 10<w<x<y<40. If x = 19, how many possible perimeters does this triangle have? (a) 5 (b) 8 (c) 13 (d) 21 (e) infinite With a normal deck of 52 playing cards, on what card dealt is the probability of getting a straight (five consecutive cards of any suit) 100%? In other words, how many cards would I have to deal to you, face down, before you tell me to stop because you know, with 100% accuracy, you have a straight? If it were three hours later it would be half as long until midnight as it would be if it were one hour earlier. What time is it now? If 1/3 = 7 in some other system, then 5/16 is equal to what in that system? Each figure contained within the largest square is also a square.
A bucket filled with water weighs 25 lbs. When one-half of the water is poured out, the bucket and remaining water weigh 13.5 lbs. How much does the bucket weigh? The three sides of a triangle have prime number lengths, w, x, and y, where 10<w<x<y<40. If x = 19, how many possible perimeters does this triangle have? (a) 5 (b) 8 (c) 13 (d) 21 (e) infinite With a normal deck of 52 playing cards, on what card dealt is the probability of getting a straight (five consecutive cards of any suit) 100%? In other words, how many cards would I have to deal to you, face down, before you tell me to stop because you know, with 100% accuracy, you have a straight? If it were three hours later it would be half as long until midnight as it would be if it were one hour earlier. What time is it now? If 1/3 = 7 in some other system, then 5/16 is equal to what in that system? Each figure contained within the largest square is also a square. If the figure below is folded back into a cube, what side is opposite the blackened square? What about opposite the transparent circle?
If the figure below is folded back into a cube, what side is opposite the blackened square? What about opposite the transparent circle? 
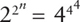 A solution for n is (a) 4 (b) 9 (c) 64 (d) 128 (e) 256 Here is a coin puzzle that may appear to have a counterintuitive answer, but I assure you it is correct. I flip a penny and a dime and hide the results from you but tell you at least one of the coins came up heads. What is the probability that both coins came up heads? The letters A U V T Y have reflection symmetry across a vertical plane. The letters H I O X have both horizontal and vertical symmetry. What capital letters have reflection symmetry across the horizontal plane only? If 10! (10 9 8 7 6 5 4 3 2 1) were to be factored into prime numbers, how many 5 s would appear? What if the number were 15!, how many 5s then?
A solution for n is (a) 4 (b) 9 (c) 64 (d) 128 (e) 256 Here is a coin puzzle that may appear to have a counterintuitive answer, but I assure you it is correct. I flip a penny and a dime and hide the results from you but tell you at least one of the coins came up heads. What is the probability that both coins came up heads? The letters A U V T Y have reflection symmetry across a vertical plane. The letters H I O X have both horizontal and vertical symmetry. What capital letters have reflection symmetry across the horizontal plane only? If 10! (10 9 8 7 6 5 4 3 2 1) were to be factored into prime numbers, how many 5 s would appear? What if the number were 15!, how many 5s then?  In the pulley system above: (a) A has a mechanical advantage of 2 and
In the pulley system above: (a) A has a mechanical advantage of 2 and In the picture, the weight of A is 20, the weight of B is 10, and the coefficient of friction f is .2 How heavy must Z be to keep A from sliding? At a recent small gathering of friends, there were nine more women than men. If the ratio of women to men was 5 to 2, how many men and women were at the party? I have a few objects I need to weigh with weights from 1 to 40 ounces. What are four weights I can use to be able to weigh any weight from 1 to 40 ounces (whole number weights only and including 1 and 40 ounces)? Im trying to keep the number of weights I buy to a minimum, so what is the least number I would have to purchase of each of these four weights to accomplish my goal? What number comes next? Remember, anything goes with sequence puzzles. 33 20 14 11 In the formula below, what is the value of g? v = f (1g)t Given five points in space, connecting three points at a time to determine a plane (extending to infinity) what is the maximum number of lines that will result from all intersections? Each figure contained within the largest square is also a square. What are the sizes of squares A, B, C, and D?
In the picture, the weight of A is 20, the weight of B is 10, and the coefficient of friction f is .2 How heavy must Z be to keep A from sliding? At a recent small gathering of friends, there were nine more women than men. If the ratio of women to men was 5 to 2, how many men and women were at the party? I have a few objects I need to weigh with weights from 1 to 40 ounces. What are four weights I can use to be able to weigh any weight from 1 to 40 ounces (whole number weights only and including 1 and 40 ounces)? Im trying to keep the number of weights I buy to a minimum, so what is the least number I would have to purchase of each of these four weights to accomplish my goal? What number comes next? Remember, anything goes with sequence puzzles. 33 20 14 11 In the formula below, what is the value of g? v = f (1g)t Given five points in space, connecting three points at a time to determine a plane (extending to infinity) what is the maximum number of lines that will result from all intersections? Each figure contained within the largest square is also a square. What are the sizes of squares A, B, C, and D? 