Martin Gardner - My Best Mathematical and Logic Puzzles

MY BEST
MATHEMATICAL
AND
LOGIC PUZZLES

Martin Gardner

DOVER PUBLICATIONS, INC.

New York

Copyright

Copyright 1994 by Martin Gardner.

All rights reserved.

Bibliographical Note

My Best Mathematical and Logic Puzzles, first published by Dover Publications, Inc., in 1994, is a new and original collection of work previously published in Scientific American, Games magazine and in earlier volume collections. A new Introduction has been written expressly for this Dover edition.

Library of Congress Cataloging-in-Publication Data

Gardner, Martin, 1914

My best mathematical and logic puzzles / Martin Gardner.

p. cm.

ISBN-13: 978-0-486-28152-0 (pbk.)

ISBN-10: 0-486-28152-3 (pbk.)

1. Mathematical recreations. I. Title.

QA95.G292 1994

Manufactured in the United States by Courier Corporation
28152315
www.doverpublications.com

INTRODUCTION

DURING the twenty-five years that I had the great privilege of writing the Mathematical Games column in Scientific American, my practice was to devote a column, about every six months, to what I called short problems or puzzles. These puzzles were, of course, mathematical rather than problems involving words. I did my best to present new and unfamiliar puzzles that were not to be found in classic collections such as the books by Sam Loyd and Henry Dudeney.

Readers were quick to catch mistakes and to supply in some cases alternate solutions or interesting generalizations. This valuable feedback was incorporated when the puzzle columns were reprinted in book collections.

Most of the problems in this book are selected from the first three collections. The last 12 puzzles are selected from two articles I contributed to Games magazine (January/February and November/December, 1978). Some have been updated by adding references to new developments related to the puzzle. Needless to say, I welcome any corrections or additions. They can be sent to me in care of the publisher, Dover Publications, 31 East 2nd Street, Mineola, N.Y. 11501.

MARTIN GARDNER

CONTENTS

AN OLD RIDDLE runs as follows. An explorer walks one mile due south, turns and walks one mile due east, turns again and walks one mile due north. He finds himself back where he started. He shoots a bear. What color is the bear? The time-honored answer is: White, because the explorer must have started at the North Pole. But not long ago someone made the discovery that the North Pole is not the only starting point that satisfies the given conditions! Can you think of any other spot on the globe from which one could walk a mile south, a mile east, a mile north and find himself back at his original location?

TWO MEN PLAY a game of draw poker in the following curious manner. They spread a deck of 52 cards face up on the table so that they can see all the cards. The first player draws a hand by picking any five cards he chooses. The second player does the same. The first player now may keep his original hand or draw up to five cards. His discards are put aside out of the game. The second player may now draw likewise. The person with the higher hand then wins. Suits have equal value, so that two flushes tie unless one is made of higher cards. After a while the players discover that the first player can always win if he draws his first hand correctly. What hand must this be?

THE PROPS FOR this problem are a chessboard and 32 dominoes. Each domino is of such size that it exactly covers two adjacent squares on the board. The 32 dominoes therefore can cover all 64 of the chessboard squares. But now suppose we cut off two squares at diagonally opposite corners of the board and discard one of the dominoes. Is it possible to place the 31 dominoes on the board so that all the remaining 62 squares are covered? If so, show how it can be done. If not, prove it impossible.

HERES A RECENT twist on an old type of logic puzzle. A logician vacationing in the South Seas finds himself on an island inhabited by the two proverbial tribes of liars and truth-tellers. Members of one tribe always tell the truth, members of the other always lie. He comes to a fork in a road and has to ask a native bystander which branch he should take to reach a village. He has no way of telling whether the native is a truth-teller or a liar. The logician thinks a moment, then asks one question only. From the reply he knows which road to take. What question does he ask?

IMAGINE THAT YOU have three boxes, one containing two black marbles, one containing two white marbles, and the third, one black marble and one white marble. The boxes were labeled for their contentsBB, WW and BWbut someone has switched the labels so that every box is now incorrectly labeled. You are allowed to take one marble at a time out of any box, without looking inside, and by this process of sampling you are to determine the contents of all three boxes. What is the smallest number of drawings needed to do this?

A CARPENTER, working with a buzz saw, wishes to cut a wooden cube, three inches on a side, into 27 one-inch cubes. He can do this easily by making six cuts through the cube, keeping the pieces together in the cube shape. Can he reduce the number of necessary cuts by rearranging the pieces after each cut?

A YOUNG MAN lives in Manhattan near a subway express station. He has two girl friends, one in Brooklyn, one in The Bronx. To visit the girl in Brooklyn he takes a train on the downtown side of the platform; to visit the girl in The Bronx he takes a train on the uptown side of the same platform. Since he likes both girls equally well, he simply takes the first train that comes along. In this way he lets chance determine whether he rides to The Bronx or to Brooklyn. The young man reaches the subway platform at a random moment each Saturday afternoon. Brooklyn and Bronx trains arrive at the station equally oftenevery 10 minutes. Yet for some obscure reason he finds himself spending most of his time with the girl in Brooklyn: in fact on the average he goes there nine times out of ten. Can you think of a good reason why the odds so heavily favor Brooklyn?

A COMMUTER IS in the habit of arriving at his suburban station each evening exactly at five oclock. His wife always meets the train and drives him home. One day he takes an earlier train, arriving at the station at four. The weather is pleasant, so instead of telephoning home he starts walking along the route always taken by his wife. They meet somewhere on the way. He gets into the car and they drive home, arriving at their house ten minutes earlier than usual. Assuming that the wife always drives at a constant speed, and that on this occasion she left just in time to meet the five oclock train, can you determine how long the husband walked before he was picked up?

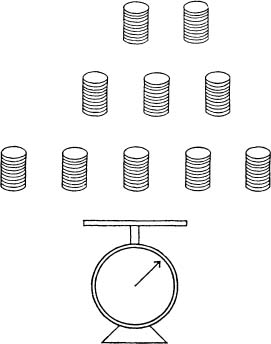
IN RECENT YEARS a number of clever coin-weighing or ball-weighing problems have aroused widespread interest. Here is a new and charmingly simple variation. You have 10 stacks of coins, each consisting of 10 half-dollars. One entire stack is counterfeit, but you do not know which one. You do know the weight of a genuine half-dollar and you are also told that each counterfeit coin weighs one gram more than it should. You may weigh the coins on a pointer scale. What is the smallest number of weighings necessary to determine which stack is counterfeit?