Naoki Inaba - The Original Area Mazes: 100 Addictive Puzzles to Solve with Simple Math―and Clever Logic!

NAOKI INABA, who was born in Nagoya in 1979, is one of the greatest puzzle inventors of all time, and he is not yet forty years old. He has already devised more types of pencil-and-paper logic puzzle than anyone else alive, and books of his area mazes have sold tens of thousands of copies in Japan. Inabas puzzle career began when he was a teenager. In the late 80s and 90s, two rival Japanese puzzle magazinesPuzzler and Nikoliboth encouraged readers to send in their own ideas. They inspired a generation of young puzzle designers, of whom Inaba became the most prolific. He was sixteen when he had his first invention published, and soon after that set up his own website where, for about ten years, he introduced a new puzzle type every week.

Like sudoku and KenKen, these puzzles were all based on grids, to be filled in using logic alone. Each puzzle type had its own rules and required different strategies to solve. Inaba is remarkable not only for the quantity of puzzle types he has invented but also for their minimalism and elegance. The rules can often be summed up in a single line. When Ryoichi Murakami, the director of El Camino coaching school in Tokyo, asked Inaba to devise a puzzle based on the areas of rectangles, he came up with menseki meiro, or area mazes. The challenge barely needs stating: Find the value of the question mark.

For a puzzle to catch on, however, it must not only have simple rules but also assume no technical expertise. Area mazes fulfill this requirement. All you need to know is that the area of a rectangle is the height times the width. No other mathematical techniques are neededindeed, all others must be relinquished, especially fractions and equations. This prohibition makes for a gorgeous and thrilling puzzle. Yes, we could plug the given values into a set of equations and solve them.

But this strategy is laborious and ugly, plus it turns the puzzle into one that can be solved by rote. Instead, area mazes force us to be nimble and find the answer in the most elegant way. Solving them requires a burst of insight, not the same old tricks. The area maze is one of only a few puzzles by Inaba that is not based on a grid, and the freedom to create examples of any shape adds an interesting unpredictability to the genre. With a sudoku, for example, there are no surprises: You might find it easy or difficult, but the path is clear. With an area maze, however, you are often surprised by the ingenuity of the solution.

The feeling of satisfaction once you solve it is doubly pleasurable. A good puzzle needs to come in all levels from easy to fiendish. Again, area mazes fit the bill. This book starts with elementary examples and ends with some that may have you scratching your head for days. Naoki Inaba has invented the perfect puzzle. Enjoy! ALEX BELLOSALEX BELLOS holds a degree in mathematics and philosophy from Oxford University.

His bestselling books include Heres Looking at Euclid and Can You Solve My Problems? He is the coauthor of two coloring books, Patterns of the Universe and Visions of the Universe. He writes a popular math blog and a puzzle blog for the Guardian. The Original Area Mazes: 100 Addictive Puzzles to Solve with Simple Mathand Clever Logic! Copyright 2011, 2017 by Gakken Publishing
Translation 2017 by Paper Crane Agency & Paper Crane Editions
Introduction 2017 by Alex Bellos
Puzzles copyright 2011, 2017 by Naoki Inaba Originally published in Japan as Menseki Meiro () by Gakken Publishing Co., Ltd, Tokyo in 2011.
First published in North America by The Experiment, LLC, in 2017. English translation rights arranged with Gakken Plus Co., Ltd., through Paper Crane Agency. All rights reserved. Except for brief passages quoted in newspaper, magazine, radio, television, or online reviews, no portion of this book may be reproduced, distributed, or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or information storage or retrieval system, without the prior written permission of the publisher.

The Experiment, LLC
220 East 23rd Street, Suite 301
New York, NY 10010-4674
theexperimentpublishing.com Many of the designations used by manufacturers and sellers to distinguish their products are claimed as trademarks. Where those designations appear in this book and The Experiment was aware of a trademark claim, the designations have been capitalized. The Experiments books are available at special discounts when purchased in bulk for premiums and sales promotions as well as for fund-raising or educational use. For details, contact us at
info@theexperimentpublishing.com. ISBN 978-1-61519-421-6
Ebook ISBN 978-1-61519-422-3 Cover design by Lidija Tomas
Text design by Sarah Schneider Manufactured in the United States of America
Distributed by Workman Publishing Company, Inc.
Distributed simultaneously in Canada by Thomas Allen & Son Ltd. 78 6 = 13 in. 78 6 = 13 in.

Find length ... 65 5 = 13 in. These are the same, so lengths and are also the same. Find length ... 6 4 = 2 in. 5 3 = 2 in. 5 3 = 2 in.

These are the same, so lengths and are also the same. The two areas with stripes have the same height and width, so they are identical. Area is 50 in.2 SOLUTION: 4 in. 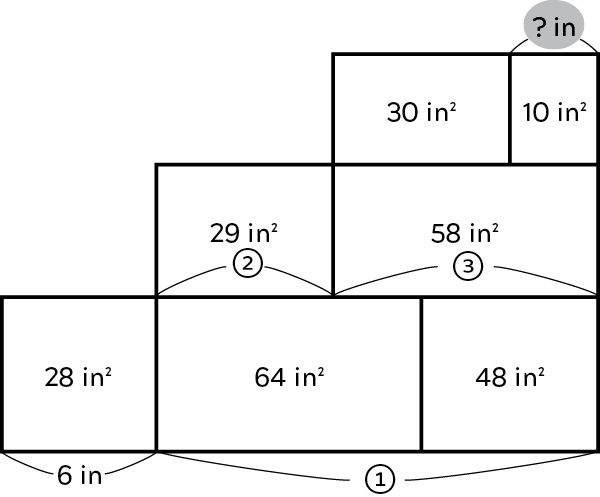Add the two areas at bottom right... 64 + 48 = 112 in.2 This is four times 28 in.2 So, length is four times 6 in.... 6 4 = 24 in.

In the middle row, 58 in.2 is double 29 in.2 So, length is double length , and length is triple length . Find length ... 24 3 = 8 in. Find length ... 24 8 = 16 in. In the top row, 30 in.2 is triple 10 in.2 So, length is four times length .

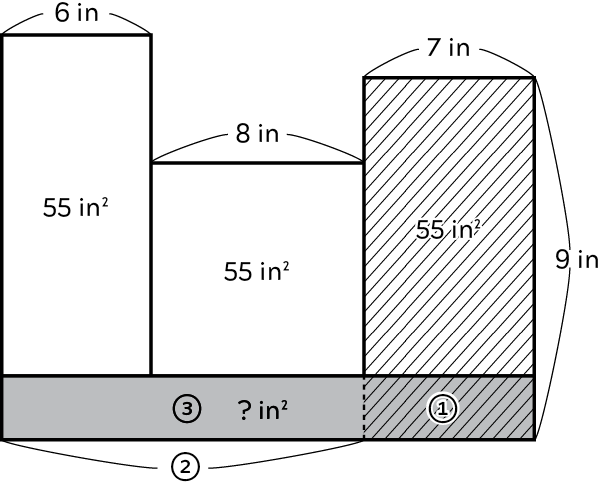Length is 16 4 = 4 in. SOLUTION: 24 in.2 Find the area with stripes... 7 9 = 63 in.2 Find area