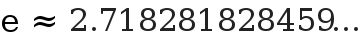Arithmetic is the branch of mathematics that most of us start with, studying numbers, their properties, and operations with those numbers. Here in this section we will be examining sets of numbers, the decimal system, order of operations, fractions, decimals, percents, proportions, and applications of these concepts.
SETS OF NUMBERS
What is a number? How many different types of numbers are there? Imagine going back in time to when numbers were first invented. What do you think they were used for at first? As we go through this imaginary journey, we will come across different sets , or groups, of numbers.
The first set that we come across is the NATURAL numbers. These are the counting numbers: 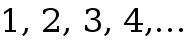 Symbolized by
Symbolized by 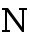 . If all we care about is counting and adding things up, this is all wed need, but theres much more. Imagine cavemen and cavewomen counting sticks and stones .
. If all we care about is counting and adding things up, this is all wed need, but theres much more. Imagine cavemen and cavewomen counting sticks and stones .
The next set is the WHOLE numbers. These include the natural numbers and the special number zero. 0 looks like a donut and a donut has a hole (whole number). 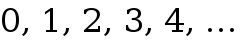 Symbolized by
Symbolized by  . In modern times, we tend to take zero for granted, but not all ancient civilizations had a concept of zero. It was invented independently in Mesopotamia, Mayan empire, and India starting around 3 BC . Besides signifying nothing, zero is important as a place holder. Without zero, we would end up like the Romans who had to have separate symbols for 1 = I , 10 = X , 100 = C , and 1000 = M. A simple number like 1999 becomes MCMXCIX.
. In modern times, we tend to take zero for granted, but not all ancient civilizations had a concept of zero. It was invented independently in Mesopotamia, Mayan empire, and India starting around 3 BC . Besides signifying nothing, zero is important as a place holder. Without zero, we would end up like the Romans who had to have separate symbols for 1 = I , 10 = X , 100 = C , and 1000 = M. A simple number like 1999 becomes MCMXCIX.
Then we start losing things, going into debt, and we need to keep track of loss. To do this we use the INTEGERS . The integers include the whole numbers and their opposites. Keep in mind that the opposite of 0 is still 0; its neutral. These integers can be listed, but they go on forever, forward and backward. ., 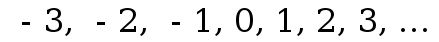 Symbolized by
Symbolized by 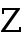 .
.


Why use a Z for integers, when it clearly starts with I ? The Z stands for the German word Zahlen , meaning numbers. Can you imagine how negative numbers were invented? Negative numbers were first used around the 7 th century AD in India to keep track of debts .
The integers are fine for most things, we can count, add, subtract, multiply, but once we start dividing, we run into trouble. Thats where the RATIONAL numbers come in. Rational comes from the root ratio, which means to cut or divide. If we have one pizza and cut it into eight parts, then we eat one slice thats  of the pizza. If we eat two slices, we have
of the pizza. If we eat two slices, we have  but thats the same as
but thats the same as  . Rational numbers include fractions that can be written using the integers. We can also write these as decimals, but the decimals either stop like
. Rational numbers include fractions that can be written using the integers. We can also write these as decimals, but the decimals either stop like 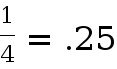 or they repeat themselves like
or they repeat themselves like  which we can also write as
which we can also write as 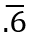 , the bar showing which digits repeat. For example,
, the bar showing which digits repeat. For example, 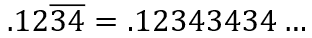 Rationals include decimals, fractions, and percents and you will learn how to convert among each of them. Rationals are symbolize by
Rationals include decimals, fractions, and percents and you will learn how to convert among each of them. Rationals are symbolize by 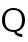 . The Q here stands for quotient.
. The Q here stands for quotient.
Since a rational is any number that can be written as a fraction using integers, the set of rational numbers also includes the integers , because any integer can be written as a fraction over 1. For example, 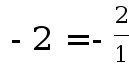 . Writing an integer this way can be helpful at times, but remember that when you give solutions, you should always reduce fractions unless otherwise stated. So far, the sets of numbers are like Russian nesting dolls. The natural numbers are the smallest set which is inside the whole numbers. The whole numbers are inside the integers. And finally, the integers are inside the largest set of the rationals.
. Writing an integer this way can be helpful at times, but remember that when you give solutions, you should always reduce fractions unless otherwise stated. So far, the sets of numbers are like Russian nesting dolls. The natural numbers are the smallest set which is inside the whole numbers. The whole numbers are inside the integers. And finally, the integers are inside the largest set of the rationals.
There is another set of numbers that is slightly crazy, the IRRATIONAL numbers. In our imaginary time travel, rational numbers and irrational numbers were probably invented in ancient Greece, usually attributed to Pythagoras . Eulers number is another example, 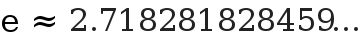







![Debra Anne Ross [Debra Anne Ross] - Master Math: Basic Math and Pre-Algebra](/uploads/posts/book/119083/thumbs/debra-anne-ross-debra-anne-ross-master-math.jpg)

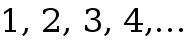 Symbolized by
Symbolized by 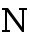 . If all we care about is counting and adding things up, this is all wed need, but theres much more. Imagine cavemen and cavewomen counting sticks and stones .
. If all we care about is counting and adding things up, this is all wed need, but theres much more. Imagine cavemen and cavewomen counting sticks and stones .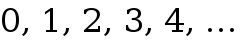 Symbolized by
Symbolized by  . In modern times, we tend to take zero for granted, but not all ancient civilizations had a concept of zero. It was invented independently in Mesopotamia, Mayan empire, and India starting around 3 BC . Besides signifying nothing, zero is important as a place holder. Without zero, we would end up like the Romans who had to have separate symbols for 1 = I , 10 = X , 100 = C , and 1000 = M. A simple number like 1999 becomes MCMXCIX.
. In modern times, we tend to take zero for granted, but not all ancient civilizations had a concept of zero. It was invented independently in Mesopotamia, Mayan empire, and India starting around 3 BC . Besides signifying nothing, zero is important as a place holder. Without zero, we would end up like the Romans who had to have separate symbols for 1 = I , 10 = X , 100 = C , and 1000 = M. A simple number like 1999 becomes MCMXCIX.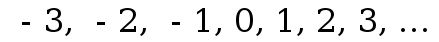 Symbolized by
Symbolized by 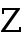 .
.

 of the pizza. If we eat two slices, we have
of the pizza. If we eat two slices, we have  but thats the same as
but thats the same as  . Rational numbers include fractions that can be written using the integers. We can also write these as decimals, but the decimals either stop like
. Rational numbers include fractions that can be written using the integers. We can also write these as decimals, but the decimals either stop like 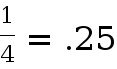 or they repeat themselves like
or they repeat themselves like  which we can also write as
which we can also write as 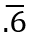 , the bar showing which digits repeat. For example,
, the bar showing which digits repeat. For example, 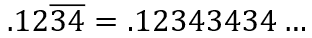 Rationals include decimals, fractions, and percents and you will learn how to convert among each of them. Rationals are symbolize by
Rationals include decimals, fractions, and percents and you will learn how to convert among each of them. Rationals are symbolize by 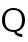 . The Q here stands for quotient.
. The Q here stands for quotient.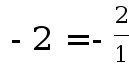 . Writing an integer this way can be helpful at times, but remember that when you give solutions, you should always reduce fractions unless otherwise stated. So far, the sets of numbers are like Russian nesting dolls. The natural numbers are the smallest set which is inside the whole numbers. The whole numbers are inside the integers. And finally, the integers are inside the largest set of the rationals.
. Writing an integer this way can be helpful at times, but remember that when you give solutions, you should always reduce fractions unless otherwise stated. So far, the sets of numbers are like Russian nesting dolls. The natural numbers are the smallest set which is inside the whole numbers. The whole numbers are inside the integers. And finally, the integers are inside the largest set of the rationals.