Prigogine - Non-equilibrium statistical mechanics

NON-EQUILIBRIUMSTATISTICAL MECHANICSILYA PRIGOGINEProfessor of Physical Chemistry and of Theoretical Physics Universit Libre, Brussels, BelgiumDOVER PUBLICATIONS, INC. MINEOLA, NEW YORK Bibliographical Note This Dover edition, first published in 2017, is an unabridged republication of the work originally published in 1962 by Interscience Publishers, New York, as Volume I of the series Monographs in Statistical Physics and Thermodynamics. Library of Congress Cataloging-in-Publication Data Names: Prigogine, I. (Ilya), author. Title: Non-equilibrium statistical mechanics / Ilya Prigogine. Description: Mineola, New York : Dover Publications, Inc., 2017. | Includes bibliographical references and index. | Includes bibliographical references and index.

Identifiers: LCCN 2016042731| ISBN 9780486815558 | ISBN 0486815552 Subjects: LCSH: Statistical mechanics. Classification: LCC QC175 .P762 2017 | DDC 530.13--dc23 LC record available at https://lccn.loc.gov/2016042731 Manufactured in the United States by LSC Communications 81555201 2017 www.doverpublications.com ContentsIntroduction 1. The earliest quantitative definition of irreversibility occurs in the formulation of the second law of thermodynamics. Here the introduction of the entropy concept permits the classification of natural events into reversible processes, in which entropy remains constant, and irreversible processes, in which entropy increases with time. The classification is purely phenomenological, however, and is clearly insufficient to establish the connection between irreversibility and the laws of mechanics. The link with mechanics first appeared through the kinetic theory of gases, whose foundation was laid down more than a hundred years ago in a rapid succession of papers by Kronig (1856), Clausius (1857), and Maxwell (I860).

These researches culminated in the famous H-theorem of Boltzmann (1872). Its fundamental importance arises from the introduction of the quantity H, defined in terms of the molecular velocity distribution function, which behaves exactly like the thermodynamic entropy. A characteristic feature of this stage of the theory was the free mixing of mechanical and probabilistic concepts. In Kronigs own words (1856): The path of each molecule must be so irregular that it will defy all calculations. However, according to the laws of probability theory, one can assume a completely regular motion instead of this completely irregular one. Such considerations also appear in Boltzmanns integro-differential equation for the rate of change of the velocity distribution.

In the absence of external forces this well-known equation takes the form 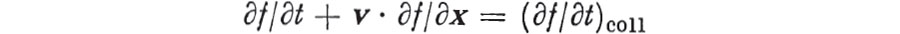Now the flow term vf/x for a system of non-interacting particles can be derived from mechanics (Liouvilles theorem). On the other hand, the collision term is not deduced from mechanics alone, but contains a probabilistic assumption about the number of collisions (the so-called Stosszahlansatz). Moreover, the collision term is estimated as though there were no flow, and the forces responsible for collisions are neglected in the flow term. There is certainly a profound physical meaning in Boltzmanns equation, as is borne out by its remarkable agreement with experiment in the calculation of transport coefficients for dilute gases. What remains unclear in Boltzmanns derivation is the range of validity of his equation. This question, as do the controversies which were raised about Boltzmanns work by Loschmidt (1876), Zermelo (1896), and others, originates in the somewhat uncritical use of probabilistic concepts.

The task of formulating a general theory of irreversible processes has acquired new urgency in recent years. The reason is not only that time, so closely related to irreversibility, remains one of the basic problems of physics, but also that there is an enormous range of experimental conditions in which transport or relaxation phenomena are now being studied. Starting from low temperature transport processes in liquid helium or in superconductors and mounting to high temperature processes in fully ionized plasmas, the range of energies covers ten powers of ten! And yet until recently all attempts to extend Boltzmanns original derivation to situations different from those for which it was derived have failed. To us the only hope for obtaining a general theory of non-equilibrium processes seems to be to reformulate the entire problem in a more systematic way on a purely mechanical basis. This will be our main goal here. 2.

One of the main purposes of such a theory is to achieve a generality comparable to that of equilibrium statistical mechanics. While the formal structure of equilibrium statistical mechanics already appears clearly in the fundamental investigations by Gibbs (see his Collected Works, 1928), its power was only recognized around 1930 when among many other advances Ursell (1928) and Mayer (1937) applied it successfully to the problem of the equation of state (see Fowler and Guggenheim, 1939). It was therefore natural to try to adopt a similar, general point of view for non-equilibrium processes and to investigate the relation between transport equations like the Boltzmann equation and the Liouville equation which is the basic equation of ensemble theory. The pioneering work in this direction is due to Yvon (1935), Born and Green (1946 and 1947), and Kirkwood (1946). These first attempts are discussed in many papers (see for example de Boer, 1948 and 1949; Prigogine, 1958; for a recent discussion of the theory of Kirkwood and his co-workers see specially Rice and Frisch, 1960), and we shall therefore not go into details here. The importance of these contributions lies in the generality of their starting point as well as, in the case of Kirkwoods theory, in the possibility of applications to dense media.

However many aspects of these theories remain obscure. Supplementary assumptions have to be introduced and no systematic way of going beyond the classical Boltzmann equation is indicated. At the time of the work of Born and Green and Kirkwood, Bogo-liubov (1946) proposed a different and very original approach. An important feature of his theory is a clear distinction between the time scales involved. We have at least two characteristic times involved: the duration of an interaction tint (1012 1013 sec) and the relaxation time, which for a dilute gas is of the order of the time between collisions (108 109 sec). Now Bogoliubov assumes that after a time of the order of tint there occurs a great simplification in the description of the system: the one-particle distribution function f1 satisfies a separate equation and the many-particle distribution functions become functionals of f1.

Using these assumptions, Bogoliubov was able to rederive Boltzmanns equation in an elegant way and indicated how at least in principle corrections due to higher densities could be obtained. It is rather remarkable that the general theory we shall develop in this monograph permits us indeed to justify Bogoliubovs assumptions for well-defined classes of initial conditions. Perhaps the first case in which the possibility of a purely mechanical theory of irreversible processes clearly appeared was the case of interacting particles in a harmonic solid. Because of their linear character, the equations of motion can then be solved exactly and it can be shown that the system approaches equilibrium as closely as is permitted by the existence of the invariants of motion. (Klein and Prigogine, 1953; a few recent papers about this subject are Hemmer, Maximon and Wergeland 1958; Mazur and Montroll, 1960). However in a harmonic system the energy of each normal mode is an invariant and an approach to thermodynamic equilibrium in the usual sense is only possible if these invariants are destroyed by anharmonic forces.