A macroscopic object we encounter in our daily life consists of an enormously large number of atoms. While the behavior of these atoms is governed by the laws of quantum mechanics, it is often acceptable to describe them by means of classical mechanics. In this chapter, we familiarize ourselves with the basic concepts of classical mechanics. From the outset, we assume that concepts such as mass, time, displacement, and force are understood on the basis of our everyday experiences without further elaboration. The role of classical mechanics, then is to explore the precise relationship among these objects in mathematical terms.
1.1 Inertial Frame
When describing physical phenomena, we need a frame of reference from which we make our observations. The mathematical expression of the laws of mechanics takes the simplest form when the frame is the so-called inertial frame of reference .
To understand what this is, imagine that you are sitting in front of your desk in your office in your building, and suppose that the desk is firmly secured to the floor and the surface of the desk is perfectly smooth and horizontal. If you place a billiard ball on the desk and remove your hand without giving any nudge to the ball, it will just sit there. If you are to give a gentle push, it will start rolling on the desk. It will continue to move in a straight line with a constant speed until it falls off at the edge of the desk. (We shall formally define the word speed in Sect..)
These observations remain valid even if your office is housed in a train moving at a constant speed on a perfectly straight and leveled railroad track. A coordinate system attached to the desk, secured either to the building or to the train, is an example of inertial frames of reference, in which an object when subjected to no net force, either stands still or keeps on moving along a straight line at a constant speed.
However, if the train housing your office is to suddenly change direction, the ball, which was previously standing still with respect to the desk, will suddenly start moving without you doing anything to it. It is certainly more difficult to describe the behavior of the ball in such a frame of reference. In fact, the coordinate system attached to the desk, in this case, is no longer an inertial frame until the train resumes its motion along a straight line at a constant speed. Unless explicitly indicated otherwise, we shall always use an inertial frame of reference.
1.2 Mechanics of a Single Particle
Systems of our eventual interest consist of the order of
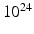
atoms, if not more. Before we tackle the problem of describing their behavior, we shall first learn how to describe a motion of a single particle. This allows us to introduce the essential concepts and terminologies needed for the studies of many-particle systems.
1.2.1 Newtons Equation of Motion
Let us take some macroscopic object such as a ball, and imagine that the size of the object becomes smaller and smaller while maintaining its original mass. The limit of this imaginary process is a point carrying certain nonzero mass. Such a point is referred to as a material point or simply a particle .
The position
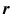
of a material point in space may change with time. This will be the case if, for example, you are to throw one such material point, for example, a ball. The time dependence of
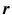
is determined by Newtons equation of motion . In an inertial frame of reference, this equation takes a particularly simple form:
where
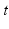
,
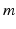
, and
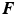
denote, respectively, the time, the mass of the material point, and the net force acting on it. Conversely, if
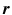
of a particle is described by () in some frame of reference, the frame is an inertial frame.
In a Cartesian coordinate system, () can be written more explicitly as
where
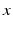
,

,
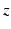
are, respectively, the
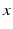
-,
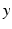
-, and
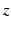
-components of the vector
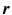
. Likewise for
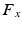
,
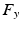
, and

.
Example 1.1
Motion under no force : If
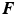
is zero at all time, then () tells us that
which may be integrated to give
When no force is acting on the material point, the vector
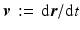
, called the velocity of the material point, is seen to be independent of time. We also observe that the material point moves along a straight line, thus confirming what was said about inertial frames of reference in Sect..














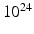 atoms, if not more. Before we tackle the problem of describing their behavior, we shall first learn how to describe a motion of a single particle. This allows us to introduce the essential concepts and terminologies needed for the studies of many-particle systems.
atoms, if not more. Before we tackle the problem of describing their behavior, we shall first learn how to describe a motion of a single particle. This allows us to introduce the essential concepts and terminologies needed for the studies of many-particle systems.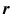 of a material point in space may change with time. This will be the case if, for example, you are to throw one such material point, for example, a ball. The time dependence of
of a material point in space may change with time. This will be the case if, for example, you are to throw one such material point, for example, a ball. The time dependence of 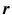 is determined by Newtons equation of motion . In an inertial frame of reference, this equation takes a particularly simple form:
is determined by Newtons equation of motion . In an inertial frame of reference, this equation takes a particularly simple form:
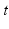 ,
, 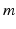 , and
, and 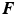 denote, respectively, the time, the mass of the material point, and the net force acting on it. Conversely, if
denote, respectively, the time, the mass of the material point, and the net force acting on it. Conversely, if 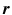 of a particle is described by () in some frame of reference, the frame is an inertial frame.
of a particle is described by () in some frame of reference, the frame is an inertial frame.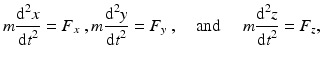
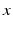 ,
,  ,
, 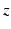 are, respectively, the
are, respectively, the 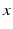 -,
-, 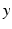 -, and
-, and 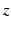 -components of the vector
-components of the vector 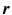 . Likewise for
. Likewise for 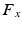 ,
, 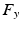 , and
, and  .
.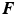 is zero at all time, then () tells us that
is zero at all time, then () tells us that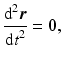
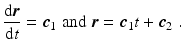
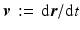 , called the velocity of the material point, is seen to be independent of time. We also observe that the material point moves along a straight line, thus confirming what was said about inertial frames of reference in Sect..
, called the velocity of the material point, is seen to be independent of time. We also observe that the material point moves along a straight line, thus confirming what was said about inertial frames of reference in Sect..