Ramin Takloo-Bighash - Right Triangles, Sums of Squares, and Arithmetic

Advisory Board:

Colin Adams, Williams College

David A. Cox, Amherst College

L. Craig Evans, University of California, Berkeley

Pamela Gorkin, Bucknell University

Roger E. Howe, Yale University

Michael E. Orrison, Harvey Mudd College

Lisette G. de Pillis, Harvey Mudd College

Jill Pipher, Brown University

Fadil Santosa, University of Minnesota

Undergraduate Texts in Mathematics are generally aimed at third- and fourth-year undergraduate mathematics students at North American universities. These texts strive to provide students and teachers with new perspectives and novel approaches. The books include motivation that guides the reader to an appreciation of interrelations among different aspects of the subject. They feature examples that illustrate key concepts as well as exercises that strengthen understanding.

More information about this series at http://www.springer.com/series/666

This Springer imprint is published by the registered company Springer Nature Switzerland AG

The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland

This book came out of an attempt to explain to a class of motivated students at the University of Illinois at Chicago what sorts of problems I thought about in my research. In the course, we had just talked about the integral solutions to the Pythagorean Equation and it seemed only natural to use the Pythagorean Equation as the context to motivate the answer. Basically, I motivated my own research, the study of rational points of bounded height on algebraic varieties, by posing the following question: What can you say about the number of right triangles with integral sides whose hypotenuses are bounded by a large number 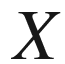? How does this number depend on 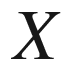? In attempting to give a truly elementary explanation of the solution, I ended up having to introduce a fair bit of number theory, the Gauss circle problem, the Mbius function, partial summation, and other topics. These topics formed the material in Chapter of the present text.

Mathematicians never develop theories in the abstract. Despite the impression given by textbooks, mathematics is a messy subject, driven by concrete problems that are unruly. Theories never present themselves in little bite-size packages with bowties on top. Theories are the afterthought. In most textbooks, theories are presented in beautiful well-defined forms, and there is in most cases no motivation to justify the development of the theory in the particular way and what example or application that is given is to a large extent artificial and just too perfect. Perhaps students are more aware of this fact than what professional mathematicians tend to give them credit forand in fact, in the case of the class I was teaching, even though the material of Chapter was fairly technical, my students responded quite well to the lectures and followed the technical details enthusiastically. Apparently, a bit of motivation helps.

What I have tried to do in this book is to begin with the experience of that class and take it a bit further. The idea is to ask natural number theoretic questions about right triangles and develop the necessary theory to answer those questions. For example, we show in Chapter .

When I was in high school, I used to think of number theory as a kind of algebra . Essentially everything I learned involved doing algebraic operations with variables, and it did not look like that number theory would have anything to do with areas of mathematics other than algebra. In reality, number theory as a field of study sits at the crossroads of many branches of mathematics, and that fact already makes a prominent appearance in this modest book. Throughout the book, there are many places where geometric, topological, and analytic considerations play a role. For example, we need to use some fairly sophisticated theorems from analysis in Chapter . If you have not learned analysis before reading this book, you should not be disheartened. If anything, you should take delight in the fact that now you have a real reason to learn whatever theorem from analysis that you may not otherwise have fully appreciated.

Each chapter of the book has a few exercises. I recommend that the reader tries all of these exercises, even though a few of them are quite difficult. Because of the nature of this book, many of the ideas are not fully developed in the text, and the exercises are included to augment the material. For example, even though the Mbius function is introduced in Chapter . Many of these exercises are problems that I have seen over the years in various texts, jotted down in my notebooks or assigned in exams, but do not remember the source. The classical textbooks by Landau [L], Carmichael [Car], and Mossaheb [M] are certainly the sources for a few of the exercises throughout the text. A few of the exercises in the book are fairly non-trivial problems. I have posted some hints for a number of the exercises on the books website at