Kenneth R. Lang - Essential Astrophysics

Essential Astrophysics — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Essential Astrophysics" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...221

Springer-Verlag Berlin Heidelberg 2013

Kenneth R. Lang Essential Astrophysics Undergraduate Lecture Notes in Physics 10.1007/978-3-642-35963-7_1

1. Observing the Universe

Kenneth R. Lang 1

(1)

Department of Physics and Astronomy, Tufts University, Medford, MA, USA

1.1 What Do Astronomers and Astrophysicists Do?

Astronomy is an ongoing, cumulative science in which astronomers either discover previously unseen constituents of the observable universe or determine physical properties of known ones. They measure the mass, luminosity, distance, size, chemical composition, motion, and magnetic fields of planets, stars, galaxies, and their surroundings.

Astrophysicists apply the laws of physics to celestial objects and events, thereby interpreting and explaining the astronomical observations. They assume that the physical laws that apply on Earth are valid throughout the Cosmos, but often under extreme conditions that cannot be achieved on our planet. The diverse aspects of physics used in astrophysics include radiation processes and universal gravitation, cosmic and particle motion, atomic and nuclear physics, and special and general relativity.

Astronomers and astrophysicists together investigate how everything in the universe originates, changes, interacts, moves, and radiates. Theoretical studies, analytical models, and numerical simulations with computers are also employed to help understand these processes.

Astronomy, and therefore astrophysics, is an instrument-driven science. Many of the seminal discoveries in astronomy have been accidental and unanticipated, often made when using unique telescopes, new technology, and novel detection equipment (Lang ). These instruments extend our vision to places that are not accessible to direct observation, enabling us to see the invisible and permitting us to look at the universe in new ways. Without a telescope, for example, the vast majority of stars cannot be seen, and all but a very few of the billions of galaxies and most of the expanding universe are invisible to the unaided eye.

Observations provide the crucial data for our celestial science. Without them, astrophysicists would have nothing to describe. Fortunately, an astronomical object can be observed over and over again, in different ways, once it has been discovered. These observations require knowledge of our location on the Earth, the location of the object in the sky, and an understanding of both angular measure and passing time.

1.2 Our Place on Earth

In order to observe cosmic objects with any accuracy, we must first establish our bearings here on Earth. In arguments used by Pythagoras (572479 BC), and subsequently recorded by Aristotle (384322 BC), it was shown that the Earth is a sphere. During a lunar eclipse, when the Moons motion carries it through the Earths shadow, observers at different locations invariably saw a curved shadow on the Moon. Only a spherical body can cast a round shape in all orientations. The curved surface of the ocean was also inferred by watching a ship disappear over the horizon; first the hull and then the mast disappear from view.

So we can, to first approximation, assume the Earth is a sphere, and locate ourselves within a grid of great circles on it. A great circle divides the sphere in half; the name derives from the fact that no greater circles can be drawn on a sphere. A great circle halfway between the North and South Poles is called the Equator because it is equally distant between both poles.

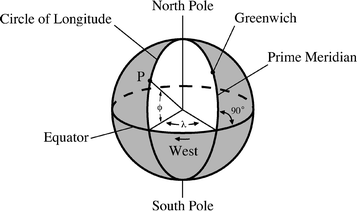
Circles of longitude are great circles that pass around the Earth from pole to pole, perpendicular to the Equator. Each circle of longitude intersects the equator in two points that are 180 apart. We halve the great circles of longitude into semicircles, called meridians. Long ago, in 1884, it was decided that the half-circle of longitude passing through the old Royal Observatory in Greenwich, England, would mark 0 longitude. It was designated as the Prime Meridian, the starting point of counting longitudes.

The longitude, denoted by the Greek letter , of any point on the Earths surface is the angle measured westward from the intersection of the Prime Meridian with the Equator to the equatorial intersection of the circle of longitude that passes through the point (Fig. ) has discussed early measurements of the size of the Earth, and the associated beginning of the metric system.

Fig. 1.1

Latitude and longitude Great circles through the North and South Poles of the Earth create circles of longitude. They are perpendicular to the Equator where they intersect it. The circle of longitude that passes through Greenwich England is called the Prime Meridian. The longitude of any point, P, is the angle lambda, , measured westward along the Equator from the intersection of the Prime Meridian with the Equator to the equatorial intersection of the circle of longitude that passes through the point. The latitude is the angle phi, , measured northward (positive) or southward (negative) along the circle of longitude from the Equator to the point. In this figure, the point P corresponds to San Francisco

Example: Location and rotation speed on the Earth

The length of the day and the rotation period is the same for every place on Earth, but the speed of rotation around its axis depends on the surface location. The surface speed of rotation is greatest at the equator and reduces to lower values at higher latitudes. Using an equatorial radius of about 6,378 km, the Earth would have to be rotating at a speed of about 464 m s1 to spin about its equatorial circumference once every 24 h. To calculate this speed, just multiply the equatorial radius by 2 to get the equatorial circumference, and divide by 24 h, where there are 86,400 s per hour. The constant = 3.1416. At higher latitudes, closer to the poles, the circumferential distance around the Earth, and perpendicular to a great circle of longitude, is less, so the speed is less. The speed diminishes to almost nothing at the geographic poles, which are pierced by the rotation axis.

Every location on the Earth rotates about an axis that pierces the Earth and extends between its North and South Poles. The period of rotation, and the length of the day, is everywhere the same, but the rotation speed is fastest at the equator and systematically lower at higher latitudes.

The geographic description of the location of an observatory includes its height, h , in meters above mean sea level. The geodetic coordinates of longitude, latitude and height, designated , , and h , are specified online in The Astronomical Almanac for all observatories engaged in professional programs of astronomical observations.

The Global Positioning System (GPS) is now used to determine reliable location and time information. It is a system of about 30 navigation satellites developed, maintained and operated by the U.S. Air Force for military and civilian purposes. Each satellite is constantly beaming radio signals that contain the exact time. These signals take a few milliseconds to travel from a satellite to the GPS receiver, and it has a built-in computer that calculates its precise position on Earth using signal time delays from four or more satellites. The time differences are converted into distance by multiplication with the speed of light, and these distances are translated by triangulation into an exact position accurate to about 100 m.

The numbers after the N (north) notation on the GPS receiver indicate its latitude, while the numbers after the W (west) notation indicates its longitude. The GPS devices used in automobiles specify the longitude and latitude of your start and end points, and map the route between them.

Next page

1234567...221

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Essential Astrophysics»

Look at similar books to Essential Astrophysics. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Steven Weinberg

Lectures on Astrophysics

Kenneth R Lang

A Brief History of Astronomy and Astrophysics

Giovanni Carraro

Astrophysics of the Interstellar Medium

Tyson Neil de Grasse

Accessory to War: The Unspoken Alliance Between Astrophysics and the Military

Tyson

Accessory to War

Tyson

Astrophysics for People in a Hurry

Spurio

PARTICLES AND ASTROPHYSICS: a multi-messenger approach

Binney

Astrophysics: A Very Short Introduction

Charles Keeton

Principles of Astrophysics

Neil deGrasse Tyson

Accessory to War: The Unspoken Alliance Between Astrophysics and the Military

Lang Lang

Lang Lang. Playing with Flying Keys

Brian Koberlein

Astrophysics Through Computation: With Mathematica® Support

Discussion, reviews of the book Essential Astrophysics and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.