Springer International Publishing Switzerland 2017
Anand Jayant Kulkarni , Ganesh Krishnasamy and Ajith Abraham Cohort Intelligence: A Socio-inspired Optimization Method Intelligent Systems Reference Library 10.1007/978-3-319-44254-9_1
1. Introduction to Optimization
1.1 What Is Optimization?
For almost all the human activities there is a desire to deliver the most with the least. For example in the business point of view maximum profit is desired from least investment; maximum number of crop yield is desired with minimum investment on fertilizers; maximizing the strength, longevity, efficiency, utilization with minimum initial investment and operational cost of various household as well as industrial equipments and machineries. To set a record in a race, for example, the aim is to do the fastest (shortest time).
The concept of optimization has great significance in both human affairs and the laws of nature which is the inherent characteristic to achieve the best or most favorable (minimum or maximum) from a given situation []. In addition, as the element of design is present in all fields of human activity, all aspects of optimization can be viewed and studied as design optimization without any loss of generality. This makes it clear that the study of design optimization can help not only in the human activity of creating optimum design of products, processes and systems, but also in the understanding and analysis of mathematical/physical phenomenon and in the solution of mathematical problems. The constraints are inherent part if the real world problems and they have to be satisfied to ensure the acceptability of the solution. There are always numerous requirements and constraints imposed on the designs of components, products, processes or systems in real-life engineering practice, just as in all other fields of design activity. Therefore, creating a feasible design under all these diverse requirements/constraints is already a difficult task, and to ensure that the feasible design created is also the best is even more difficult.
1.1.1 General Problem Statement
All the optimal design problems can be expressed in a standard general form stated as follows:
A problem where the objective function is to be maximized (instead of minimized) can also be handled with this standard problem statement since maximization of a function
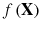
is the same as minimizing the negative of
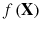
.
Similarly, the type of inequality constraints can be treated by reversing the sign of the constraint function to form the type of inequality.
Sometimes there may be simple limits on the allowable range of value a design variable can take, and these are known as side constraints:
where
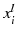
and
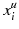
are the lower and upper limits of
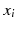
, respectively. However, these side constraints can be easily converted into the normal inequality constraints (by splitting them into 2 inequality constraints).
Although all optimal design problems can be expressed in the above standard form, some categories of problems may be expressed in alternative specialized forms for greater convenience and efficiency.
1.1.2 Active/Inactive/Violated Constraints
The constraints in an optimal design problem restrict the entire design space into smaller subset known as the feasible region, i.e. not every point in the design space is feasible. See Fig..
Fig. 1.1
Active/Inactive/Violated constraints
An inequality constraint
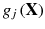
is said to be violated at the point x if it is not satisfied there
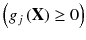
.
If
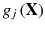
is strictly satisfied
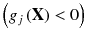
then it is said to be inactive at x.
If
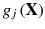
is satisfied at equality
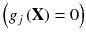
then it is said to be active at x.
The set of points at which an inequality constraint is active forms a constraint boundary which separates the feasibility region of points from the infeasible region.
Based on the above definitions, equality constraints can only be either violated
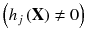
or active
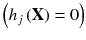
at any point x.
The set of points where an equality constraint is active forms a sort of boundary both sides of which are infeasible.
1.1.3 Global and Local Minimum Points












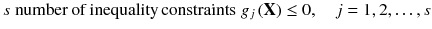
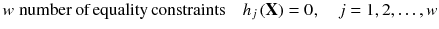
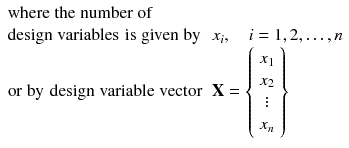
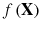 is the same as minimizing the negative of
is the same as minimizing the negative of 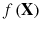 .
.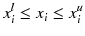
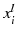 and
and 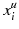 are the lower and upper limits of
are the lower and upper limits of 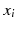 , respectively. However, these side constraints can be easily converted into the normal inequality constraints (by splitting them into 2 inequality constraints).
, respectively. However, these side constraints can be easily converted into the normal inequality constraints (by splitting them into 2 inequality constraints).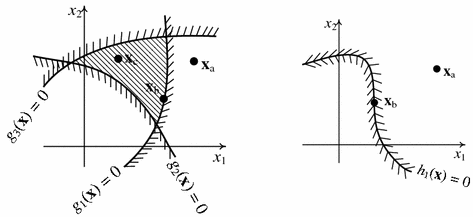
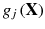 is said to be violated at the point x if it is not satisfied there
is said to be violated at the point x if it is not satisfied there 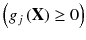 .
.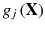 is strictly satisfied
is strictly satisfied 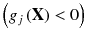 then it is said to be inactive at x.
then it is said to be inactive at x.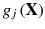 is satisfied at equality
is satisfied at equality 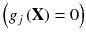 then it is said to be active at x.
then it is said to be active at x.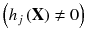 or active
or active 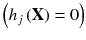 at any point x.
at any point x.