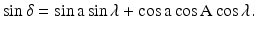Giulio Magli - Archaeoastronomy: Introduction to the Science of Stars and Stones

School of Civil Architecture, Politecnico di Milano, Milan, Italy

Giulio Magli

Email:

Today we explore the sky with powerful instruments and we know that there are millions of galaxies in the universe, each containing billions of stars. We are accustomed to thinking about the universe from an unprivileged point of view. We know, moreover, that the Sun is only one among billions of stars, and a pretty bog standard one at that, and that it occupies a relatively insignificant position in one of the branchesitself quite bog standardof one of those galaxies: the Milky Way.

Many ancient cultures acquired a profound knowledge of the sky independently, but the celestial bodies available for their observations were only those visible with the naked human eye. Furthermore, their point of view was always that of an observer who is located on an objectthe Earthwhich is subject to a complex series of motions of its own. The continual changes in the sky observed by them were, therefore, for the most part, due to apparent movements. In spite of this, many ancient astronomers devised ingenious methods of observation and made highly accurate measurements, which were reflected and exploited in the projects of the monumental architecture of their historical epochs. Thus if we want to understand these (in some cases fundamental) aspects of architecture, we must first study and understand astronomy as they did: with the naked eye, and from the Earths surface.

The centre of mass of our planet moves on an ellipse, with the Sun located at one focus. The plane which contains the Sun and the orbit of the Earth is called the Ecliptic . The Earths axis is not perpendicular to the Ecliptic, but is (today) inclined by 2330; this angle is called obliquity and denoted with the Greek letter . Since the Earths axis wobbles slightly, the value of the obliquity is not strictly constant. It varies between 25 and 22, currently diminishing at a rate of about 48 per century, so that it was 30 greater 4000 years ago (Aveni ).

Consider now a fixed observer on the Earths surface. The observer sees all heavenly bodies move as a consequence of his own movements, in particular, the daily terrestrial rotation. The observers viewpoint is a classic example of a very poor frame of reference in Mechanics, since the complicated amalgam of our planets movements give rise to quite complicated relative dynamics (a much better viewpoint would, of course, be from a spacecraft that is stationary in relation to the solar system).

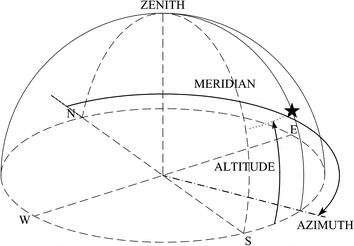
To become acquainted with a reference system, one needs a system of coordinates, that is, a set of numbers which allows one to identify unambiguously the position of any object. The observer on the Earth sees the sky as a spherical surface, the celestial sphere. In other words, he is generally unable to discern if, for instance, two stars which appear to be close in the sky are really close in the radial direction or not. Since to fix a point on a sphere only two numbers are needed (for instance, latitude and longitude on the Earth), each system of celestial coordinates will associate two numerical values to any object seen in the sky at a certain time. There are two systems of coordinates which are commonly used (and useful) in archaeoastronomy. The simpler one is the azimuth-altitude system; to visualise it, imagine first projecting the course of the Earth axis onto the celestial sphere. There will be a ideal point of intersection in the sky which we shall call the celestial pole (north or south depending on the hemisphere of the observer; but to simplify matters, unless otherwise specified, I shall refer to the north pole from now on). This ideal point is of fundamental importance; indeed, since our own reference system is rotating around the Earths axis, we see everything in the sky rotating around the pole. Now, we should imagine lowering the perpendicular to the horizon from the celestial pole. In this way, we can identify a point on the horizon and a direction on the ground towards it: these are known as geographical north and the meridian . Given a point S in the sky, whose coordinates we wish to find, we now imagine tracing the vertical plane which passes through this point. This plane intersects the horizon of the observer at a point, say S*; the azimuth A is the angle between north and the point S* on the horizon, counting positively from north to east (in other words, clockwise), and the altitude a is the angle measured on the vertical circle from S* to S (Fig. ). In particular, the altitude reached by a star when it passes the celestial meridian, that is, the ideal projection of the observers meridian into the sky, is called culmination . Of course, the celestial pole is located on the meridian; it thus has a constant azimuth (zero) and a constant altitude which, as is easy to see, equals the latitude of the observer.

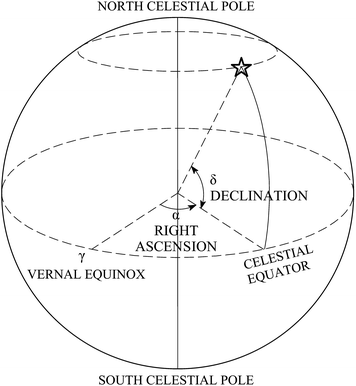
The second system of coordinates we need to use does not depend on the choice of our terrestrial observer. This system is easily understood if one imagines measuring the latitude and longitude of a point on the celestial sphere. The angular distance of the point from the celestial equator gives an angle called declination ; the analogue of the longitude is called right ascension , and it is conventionally measured from a point (the vernal equinox) along the celestial equator to the maximal circle passing through the pole and the point (Fig. ).

The right ascension-declination system has, for the archaeoastronomer, two important advantages. First of all, to know where an object was located in the sky in a certain period in the past, only one number is needed, namely, declination. Furthermore, declination is independent from the latitude of the observer, while the azimuth is. It is, therefore, important to be able to treat experimental data (usually acquired using the azimuth-altitude system) in terms of declinations. This is done using mathematical formulae which connect the two systems; one very useful formula for us is the one giving the (sinus of) the declination of a star as a function of azimuth and altitude, once the latitude of the observer is known:

A stable star, of which there are billions in the universe, can be broadly described as a huge sphere of plasma, that is, a (globally neutral) medium where all the particles are unbound and charged. Gravity tends to shrink (the technical term is collapse) the object, but thermonuclear reactions take place, which in turn produce a radiation pressure which balances the contraction. As a consequence, a standard star is in a stable state that might well last billions of years, until its nuclear fuel has been consumed. An example of a stable star is, unsurprisingly, the one that assures life on Earth, the Sun.