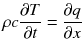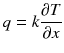1. Introduction
1.1 Introduction
Transport phenomena deals with the movement of bulk mass, energy, or a chemical component. A transport network model may be used to solve the flow rate of (1) a substance; or (2) the mechanical energy; or (3) heat; or (4) the momentum of mass; or the coupled flows of all (1)(4) together. Problems to be solved may involve simple fluid mechanics; heat transfer; moisture, or contaminant mass transport problems; or their combinations with interactions. Practical questions may arise from analyzing or designing mine ventilation and climatization; heat exchangers; solar heating plants; building heating and cooling; power plants; or chemical processing.
The theory of transport processes comes from a broad area of science and engineering. The basic approach to problem solution starts with the governing equations of the transport processes followed by differential calculus and completed by some form of numerical methods.
The time-dependent transport for any substance is generally governed by second-order partial differential equations. The simplest example is heat conduction in one dimension, described by Fouriers equation
where
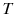
,
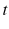
and
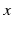
are temperature, time, and distance variables;
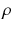
,
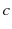
and
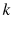
are material properties of density, specific heat, and thermal conductivity, respectively. A heat-flow network method may represent a first-order numerical solution to Eq. () with two variables, temperature, and heat flux, gives
In Eq. (). Since different transport processes often have different characteristics such as propagation velocity or interactions with other process elements, such as by mixing, it is advantageous to keep them separated from the beginning. A network model provides a natural separation and involves first-order differential equations with their specific characteristics. However, once they are combined into second-order, partial differential equations, the original characteristics are lost and with them the conservation laws may be violated during finite-difference numerical solutions. To avoid this pitfall, the transport network models will be based on finite volumes in which the Eulerian and the Lagrangean description of fluid motion will be combined.
In general, a network model is formulated in state-space form (Hangos et al. 2004) in which the space has two state variables: potential and current, related to the first derivative of the potential. In the model space, the spatial, 3D variations define a set of state variables, taken at the network nodes. Time variations make both state variables time dependent. The State-Flux (SF) name is used for the network model in the book, distinguishing the potential as the first element of the state (such as pressure, temperature, humidity, or species concentrations) from the second element, flux, as the spatial derivative (divergence, gradient or Jacobian) of the state.
The fundamental advantage of a network model as a special type of state-space model is that the conservation of current is built into it during model formulation. Another advantage is that the second-order systems for heat, mass, and momentum transport are described with a set of first-order equations. In comparison, a computational model that uses only the potential as one state variable must include the conservation of flux in separate equation. In addition, in conventional, transport solution schemes, all governing equations are in second-order, partial differential equation form, whereas the network model solution is reduced to a set of first-order differential equations.
System models (Bestion 2010) are similar to SF models, often used to solve these problems in nuclear reactor applications. Computational fluid dynamics (CFD) numerical models are even more widely used, but they apply very different numerical techniques from the network models described in this book.
Elements of a SF transport network model may also be connected to a domain of continuum model of transport processes not in the form of a network model. Continuum models are well developed and are outside the interest of network model applications which typically involve only a few tens or hundreds of thousands of nodes. The size of continuum models may be in the number of millions, or up to hundreds of millions of nodes and typically cover only a relatively small area or volume. Such a domain may be modeled outside the SF network model, solved for example by a CFD model such as ANSYS Fluent or Cradle (2012), or a Porous-Media Thermal Hydrologic (PMTH) model such as TOUGH2 or NUFT (Pruess et al. 1999, Nitao 2000). The SF network model may be coupled to an outside CFD or PMTM element with a special technique called Numerical Transport Code Functionalization (NTCF, Danko 2006), a topic of the extended book, dealing with subsurface heat and mass transport model applications.
The problem of hot working conditions in subsurface openings has been present ever since man started underground mining. Mines are getting deeper and hotter worldwide. The deepest metal mines have exceeded 4,000 m depth into the earths crust where the virgin rock temperature is near the boiling point of water. The interest in high temperature applications has further increased recently with the application of subsurface facilities to store nuclear waste material. In the emplacement area of heat-generating nuclear, spent fuel in geologic repositories may reach above-boiling temperature of water without cooling enhancement. Ventilation for cooling and environmental control is necessary in these facilities during construction and reentry operations. Other subsurface engineering applications may not need a habitable working environment, yet deal with heat transport and high temperature. Such application examples are geothermal energy production; secondary oil recovery; storage of carbon dioxide; storage of other gases including compressed air for energy buffering, and the development of deep subsurface space for many other purposes.









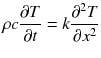
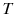 ,
, 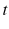 and
and 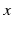 are temperature, time, and distance variables;
are temperature, time, and distance variables; 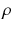 ,
, 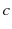 and
and 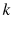 are material properties of density, specific heat, and thermal conductivity, respectively. A heat-flow network method may represent a first-order numerical solution to Eq. () with two variables, temperature, and heat flux, gives
are material properties of density, specific heat, and thermal conductivity, respectively. A heat-flow network method may represent a first-order numerical solution to Eq. () with two variables, temperature, and heat flux, gives