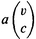The development of mathematics in the direction of greater exactness hasas is well knownled to large tracts of it becoming formalized, so that proofs can be carried out according to a few mechanical rules. The most comprehensive formal systems yet set up are, on the one hand, the system of Principia Mathematica (PM) provided that thereby no false propositions of the kind described in footnote 4 become provable.
Before going into details, we shall first indicate the main lines of the proof, naturally without laying claim to exactness. The formulae of a formal systemwe restrict ourselves here to the system PMare, looked at from outside, finite series of basic signs (variables, logical constants and brackets or separation points), and it is easy to state precisely just which series of basic signs are meaningful formulae and which are not. a formula F () of PMfor examplewith one free variable (of the type of a series of numbers), such that F ()interpreted as to contentstates: is a provable formula. We now obtain an undecidable proposition of the system PM, i.e. a proposition A, for which neither A nor not-A are provable, in the following manner:
A formula of PM with just one free variable, and that of the type of the natural numbers (class of classes), we shall designate a class-sign. We think of the class-signs as being somehow arranged in a series, and denote the n- th one by R ( n ); and we note that the concept class-sign as well as the ordering relation R are definable in the system PM. Let be any class-sign; by [ ; n ] we designate that formula which is derived on replacing the free variable in the class-sign by the sign for the natural number n. The three-term relation x = [ y ; z ] also proves to be definable in PM. We now define a class K of natural numbers, as follows:
(where Bew x means: x is a provable formula). Since the concepts which appear in the definiens are all definable in PM, so too is the concept K which is constituted from them, i.e. there is a class-sign S, such that the formula [ S; n ]interpreted as to its contentstates that the natural number n belongs to K. S, being a class-sign, is identical with some determinate R ( q ), i.e.
S = R ( q )
holds for some determinate natural number q. We now show that the proposition [ R ( q ); q ]is undecidable in PM. For supposing the proposition [ R ( q ); q ] were provable, it would also be correct; but that means, as has been said, that q would belong to K, i.e. according to (1), 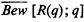 would hold good, in contradiction to our initial assumption. If, on the contrary, the negation of [ R ( q ); q ] were provable, then
would hold good, in contradiction to our initial assumption. If, on the contrary, the negation of [ R ( q ); q ] were provable, then 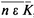 i.e. Bew [ R ( q ); q ] would hold good. [ R ( q ); q ] would thus be provable at the same time as its negation, which again is impossible.
i.e. Bew [ R ( q ); q ] would hold good. [ R ( q ); q ] would thus be provable at the same time as its negation, which again is impossible.
The analogy between this result and Richards antinomy leaps to the eye; there is also a close relationship with the liar antinomy, The method of proof just exhibited can clearly be applied to every formal system having the following features: firstly, interpreted as to content, it disposes of sufficient means of expression to define the concepts occurring in the above argument (in particular the concept provable formula); secondly, every provable formula in it is also correct as regards content. The exact statement of the above proof, which now follows, will have among others the task of substituting for the second of these assumptions a purely formal and much weaker one.
From the remark that [ R ( q ); q ] asserts its own unprovability, it follows at once that [ R ( q ); q ] is correct, since [ R ( q ); q ] is certainly unprovable (because undecidable). So the proposition which is undecidable in the system PM yet turns out to be decided by metamathematical considerations. The close analysis of this remarkable circumstance leads to surprising results concerning proofs of consistency of formal systems, which are dealt with in more detail in Section 4 (Proposition XI).
We proceed now to the rigorous development of the proof sketched above, and begin by giving an exact description of the formal system P, for which we seek to demonstrate the existence of undecidable propositions. P is essentially the system obtained by superimposing on the Peano axioms the logic of PM (numbers as individuals, relation of successor as undefined basic concept).
The basic signs of the system P are the following:
I. Constants: (not), (or), (for all), 0 (nought), (the successor of), (, ) (brackets).
II. Variables of first type (for individuals, i.e. natural numbers including 0) : x 1, y 1, z 1,....
Variables of second type (for classes of individuals): x 2 , y 2 , z 2.....
Variables of third type (for classes of classes of individuals): x 3, y 3, z 3,... and so on for every natural number as type.
Note: Variables for two-termed and many-termed functions (relations) are superfluous as basic signs, since relations can be defined as classes of ordered pairs and ordered pairs again as classes of classes, e.g. the ordered pair a, b by (( a ), ( a, b )), where ( x, y ) means the class whose only elements are x and y, and ( x ) the class whose only element is x.
By a sign of first type we understand a combination of signs of the form:
a, fa, ffa, fffa ... etc.
where a is either 0 or a variable of first type. In the former case we call such a sign a number-sign. For n > 1 we understand by a sign of n -th type the same as variable of n -th type. Combinations of signs of the form a ( b ), where b is a sign of n -th and a a sign of ( n +1 )-th type, we call elementary formulae. The class of formulae we define as the smallest class We term ( a ) ( b ) the disjunction of a and b, (a ) the negation and x ( a ) a generalization of a. A formula in which there is no free variable is called a propositional formula (free variable being defined in the usual way). A formula with just n free individual variables (and otherwise no free variables) we call an n -place relation-sign and for n = 1 also a class-sign.
By Subst 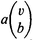 (where a stands for a formula, a variable and b a sign of the same type as ) we understand the formula derived from a , when we replace in it, wherever it is free, by b . We say that a formula a is a type-lift of another one b , if a derives from b , when we increase by the same amount the type of all variables appearing in b .
(where a stands for a formula, a variable and b a sign of the same type as ) we understand the formula derived from a , when we replace in it, wherever it is free, by b . We say that a formula a is a type-lift of another one b , if a derives from b , when we increase by the same amount the type of all variables appearing in b .
The following formulae (1-V) are called axioms (they are set out with the help of the customarily defined abbreviations: ., , , ( Ex ), =,:
I.
- (f x 1 =0)
- fx 1 = fy 1 x 1, = y 1
- x 2(0) . x 1 ( x 2( x 1) x 2( x 1)) x 1 ( x 2( x 1))
II. Every formula derived from the following schemata by substitution of any formulae for p, q and r .
- p p p
- p p q
- p q q p
- ( p q) (r p r q )
III. Every formula derived from the two schemata
- ( a ) Subst
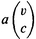
- ( b a ) b ( a )
by making the following substitutions for a, , b, c (and carrying out in 1 the operation denoted by Subst): for a any given formula, for any variable, for b any formula in which does not appear free, for c a sign of the same type as , provided that c contains no variable which is bound in a at a place where is free.















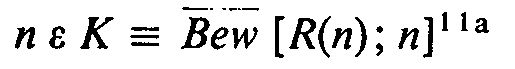
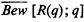 would hold good, in contradiction to our initial assumption. If, on the contrary, the negation of [ R ( q ); q ] were provable, then
would hold good, in contradiction to our initial assumption. If, on the contrary, the negation of [ R ( q ); q ] were provable, then 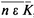 i.e. Bew [ R ( q ); q ] would hold good. [ R ( q ); q ] would thus be provable at the same time as its negation, which again is impossible.
i.e. Bew [ R ( q ); q ] would hold good. [ R ( q ); q ] would thus be provable at the same time as its negation, which again is impossible.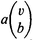 (where a stands for a formula, a variable and b a sign of the same type as ) we understand the formula derived from a , when we replace in it, wherever it is free, by b . We say that a formula a is a type-lift of another one b , if a derives from b , when we increase by the same amount the type of all variables appearing in b .
(where a stands for a formula, a variable and b a sign of the same type as ) we understand the formula derived from a , when we replace in it, wherever it is free, by b . We say that a formula a is a type-lift of another one b , if a derives from b , when we increase by the same amount the type of all variables appearing in b .