Cajic - An Illustrative Introduction to Algorithms
Here you can read online Cajic - An Illustrative Introduction to Algorithms full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2019, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.

An Illustrative Introduction to Algorithms: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "An Illustrative Introduction to Algorithms" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Cajic: author's other books
Who wrote An Illustrative Introduction to Algorithms? Find out the surname, the name of the author of the book and a list of all author's works by series.
An Illustrative Introduction to Algorithms — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "An Illustrative Introduction to Algorithms" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:

All rights reserved. This book or any portion thereof may not be reproduced or used in any manner whatsoever without the express written permission of the copyright owner except for the use of brief quotations in a book review.
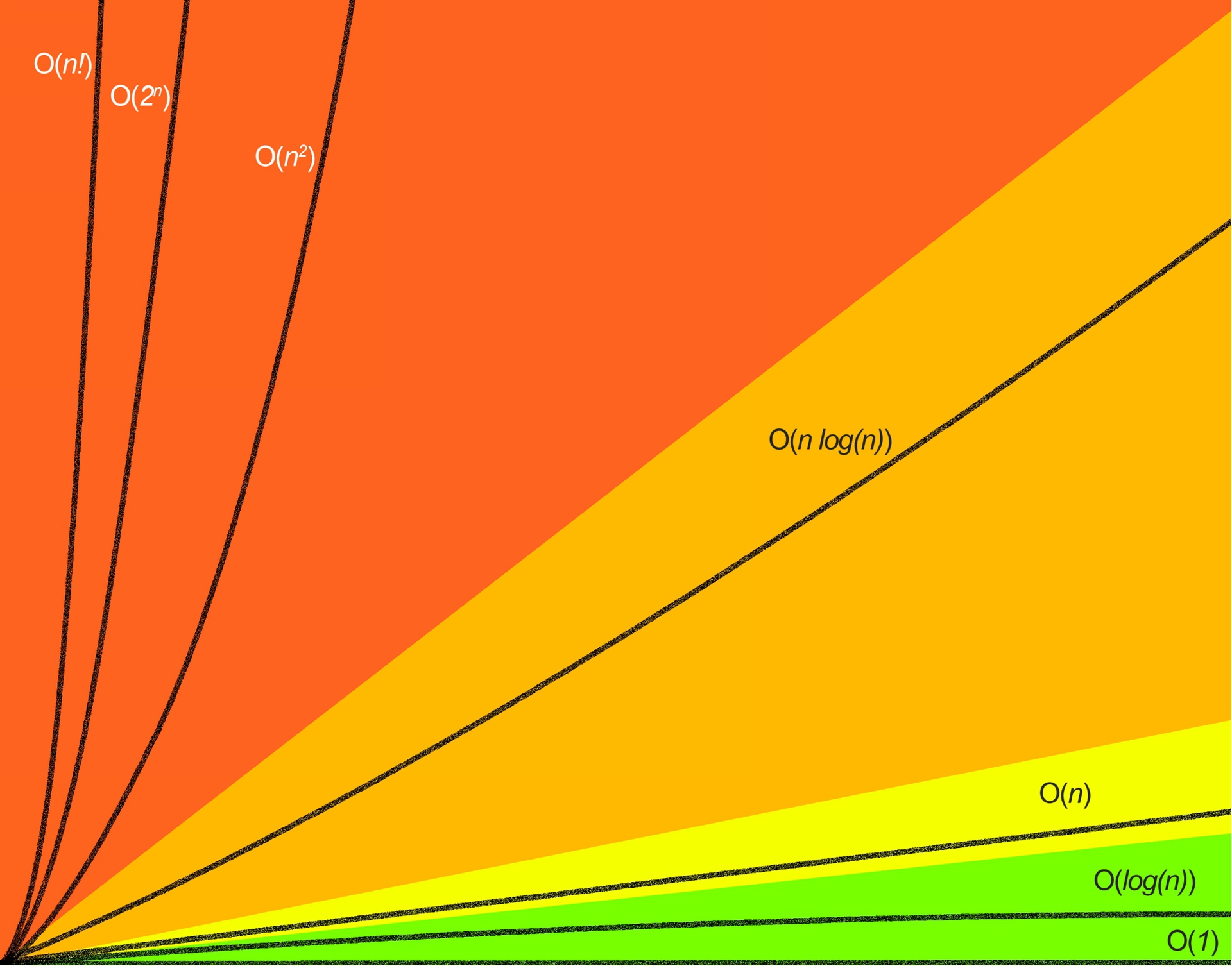
ALGORITHM | BEST | AVERAGE | BIG O |
Binary Tree Search In-Pre-Post- Order | ( n ) | ( n ) | O( n ) |
Binary Search | ( ) | ( log(n) ) | O( log(n) ) |
Bubble Sort | ( n ) | ( n ) | O( n ) |
Breadth First Search (BFS) | ( |V| + |E| ) | ( |V| + |E| ) | O( |V| * |V| ) |
Depth First Search (DFS) Directed Graph | ( |V| + |E| ) | ( |V| + |E| ) | O( |V| + |E| ) |
Depth First Search (DFS) Undirected Graph | ( |V| + |E| ) | ( |V| + |E| ) | O( |V| + 2|E| ) |
Heap Sort | ( n ) | ( n log(n) ) | O( n log(n) ) |
Insertion Sort | ( n ) | ( n ) | O( n ) |
Kruskals Algorithm | ( E log(E) ) | ( E log(E) ) | O( E log(E) ) |
Merge Sort | ( n log(n) ) | ( n log(n) ) | O( n log(n) ) |
Prims Algorithm | ( V log(V) ) | ( E log(V) ) | O( V log(V) ) |
Quick Sort | ( n log(n) ) | ( n log(n) ) | O( n ) |
Selection Sort | ( n ) | ( n ) | O( n ) |
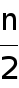 ) + O(1)
) + O(1)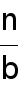 )+ O(n c ) with T(0) = and T(1) = (1) . There are three conditions to the master theorem:
)+ O(n c ) with T(0) = and T(1) = (1) . There are three conditions to the master theorem:- If c < log b a, then T(n) = (n log b a )
- If c = log b a, then T(n) = (n c logn)
- If c > log b a, then T(n) = (n c )
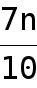 ) + n
) + nlog 10/7 1 < n, therefore T(n) = (n)
Font size:
Interval:
Bookmark:
Similar books «An Illustrative Introduction to Algorithms»
Look at similar books to An Illustrative Introduction to Algorithms. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book An Illustrative Introduction to Algorithms and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.



