This chapter will introduce some of the basic themes of the book. The geometry we are interested in concerns affine varieties , which are curves and surfaces (and higher dimensional objects) defined by polynomial equations. To understand affine varieties, we will need some algebra, and in particular, we will need to study ideals in the polynomial ring k [ x 1,, x n ]. Finally, we will discuss polynomials in one variable to illustrate the role played by algorithms .
Polynomials and Affine Space
To link algebra and geometry, we will study polynomials over a field. We all know what polynomials are, but the term field may be unfamiliar. The basic intuition is that a field is a set where one can define addition, subtraction, multiplication, and division with the usual properties. Standard examples are the real numbers
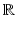
and the complex numbers
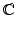
, whereas the integers
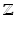
are not a field since division fails (3 and 2 are integers, but their quotient 32 is not). A formal definition of field may be found in Appendix A.
One reason that fields are important is that linear algebra works over any field. Thus, even if your linear algebra course restricted the scalars to lie in
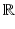
or
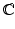
, most of the theorems and techniques you learned apply to an arbitrary field k . In this book, we will employ different fields for different purposes. The most commonly used fields will be:
The rational numbers
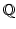
: the field for most of our computer examples.
The real numbers
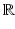
: the field for drawing pictures of curves and surfaces.
The complex numbers
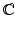
: the field for proving many of our theorems.
On occasion, we will encounter other fields, such as fields of rational functions (which will be defined later). There is also a very interesting theory of finite fieldssee the exercises for one of the simpler examples.
We can now define polynomials. The reader certainly is familiar with polynomials in one and two variables, but we will need to discuss polynomials in n variables
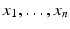
with coefficients in an arbitrary field k . We start by defining monomials.
Definition 1.
A monomial in
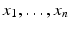
is a product of the form
where all of the exponents
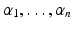
are nonnegative integers. The total degree of this monomial is the sum
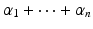
.
We can simplify the notation for monomials as follows: let
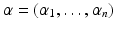
be an n -tuple of nonnegative integers. Then we set
When
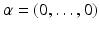
, note that x =1. We also let
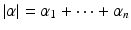
denote the total degree of the monomial x .
Definition 2.
A polynomial f in
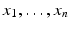
with coefficients in a field k is a finite linear combination (with coefficients in k ) of monomials. We will write a polynomial f in the form
where the sum is over a finite number of n -tuples
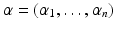
. The set of all polynomials in
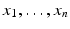
with coefficients in k is denoted
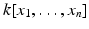
.
When dealing with polynomials in a small number of variables, we will usually dispense with subscripts. Thus, polynomials in one, two, and three variables lie in k [ x ], k [ x , y ], and k [ x , y , z ], respectively. For example,
is a polynomial in
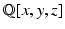
. We will usually use the letters f , g , h , p , q , r to refer to polynomials.
We will use the following terminology in dealing with polynomials.
Definition 3.
Let
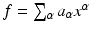
be a polynomial in
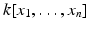
.
(i)
We call a the coefficient of the monomial x .
(ii)
If
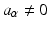
, then we call a x a term of f .
(iii)
The total degree of f 0, denoted deg( f ), is the maximum||such that the coefficient a is nonzero. The total degree of the zero polynomial is undefined.
As an example, the polynomial
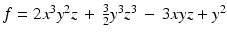
given above has four terms and total degree six. Note that there are two terms of maximal total degree, which is something that cannot happen for polynomials of one variable. In Chapter , we will study how to order the terms of a polynomial.












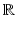 and the complex numbers
and the complex numbers 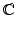 , whereas the integers
, whereas the integers 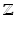 are not a field since division fails (3 and 2 are integers, but their quotient 32 is not). A formal definition of field may be found in Appendix A.
are not a field since division fails (3 and 2 are integers, but their quotient 32 is not). A formal definition of field may be found in Appendix A.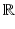 or
or 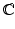 , most of the theorems and techniques you learned apply to an arbitrary field k . In this book, we will employ different fields for different purposes. The most commonly used fields will be:
, most of the theorems and techniques you learned apply to an arbitrary field k . In this book, we will employ different fields for different purposes. The most commonly used fields will be: 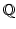 : the field for most of our computer examples.
: the field for most of our computer examples.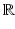 : the field for drawing pictures of curves and surfaces.
: the field for drawing pictures of curves and surfaces.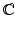 : the field for proving many of our theorems.
: the field for proving many of our theorems.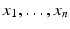 with coefficients in an arbitrary field k . We start by defining monomials.
with coefficients in an arbitrary field k . We start by defining monomials.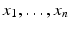 is a product of the form
is a product of the form 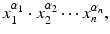
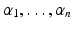 are nonnegative integers. The total degree of this monomial is the sum
are nonnegative integers. The total degree of this monomial is the sum 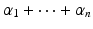 .
.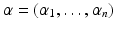 be an n -tuple of nonnegative integers. Then we set
be an n -tuple of nonnegative integers. Then we set 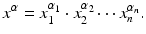
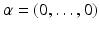 , note that x =1. We also let
, note that x =1. We also let 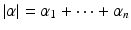 denote the total degree of the monomial x .
denote the total degree of the monomial x .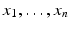 with coefficients in a field k is a finite linear combination (with coefficients in k ) of monomials. We will write a polynomial f in the form
with coefficients in a field k is a finite linear combination (with coefficients in k ) of monomials. We will write a polynomial f in the form 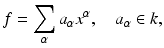
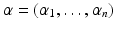 . The set of all polynomials in
. The set of all polynomials in 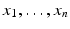 with coefficients in k is denoted
with coefficients in k is denoted 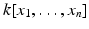 .
.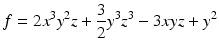
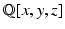 . We will usually use the letters f , g , h , p , q , r to refer to polynomials.
. We will usually use the letters f , g , h , p , q , r to refer to polynomials.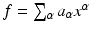 be a polynomial in
be a polynomial in 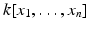 .
. 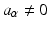 , then we call a x a term of f .
, then we call a x a term of f .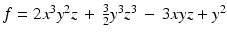 given above has four terms and total degree six. Note that there are two terms of maximal total degree, which is something that cannot happen for polynomials of one variable. In Chapter , we will study how to order the terms of a polynomial.
given above has four terms and total degree six. Note that there are two terms of maximal total degree, which is something that cannot happen for polynomials of one variable. In Chapter , we will study how to order the terms of a polynomial.