1.1 General Presentation
Usually, in the literature, only the real domain is investigated when designing and studying chaotic systems. Such research works are grouped under the name of real domain chaotic systems (RDCSs); they mainly encompass two distinct approaches: the continuous-time systems and discrete-time chaotic ones. The former are constituted by differential state equations, whereas the latter are based on iterative equations. Well-known Chen, Chua, and Lorenz systems [] are well-known examples of the second category.
It is unnecessary to exhibit a complex structure for a chaotic system to have, mathematically speaking, a complex dynamics: expansivity, sensitivity to initial conditions, topological mixing, decaying autocorrelation function, and so on [].
There is, however, a real problem with such an approach, related to the implementation of a chaotic phenomenon, no matter the considered device: the associated chaotic system is discretized both spatially and temporally. In other words, the system becomes both a discrete-valued and discrete-time pseudochaotic system, on a finite spatial lattice and for discrete times []. In this book, by digital chaos, we mean the exact result of these discretized iterations on digital computers.
In digital finite state machines, finite word lengths imply finite precision. This may lead to important dynamic degradation: nonideal distribution and correlation, short cycle length, low linear complexity, and so on [], whereas mathematical chaos definitions such as the reputed Devaneys one are compatible with finite precision domains.
Even though numerous research works have recently been published, targeting a disclosure of the degradation characteristic for some simple digital domain chaotic maps (including the piecewise linear chaotic []. Obviously, the proposed system only manipulates finite sets of integers, therefore the issue related to finite precision does not occur. Indeed, as there is no need to transform real numbers to binary sequences, CIs-based systems can be considered one of the most effective solutions to resolve the aforementioned degradation problem in digital chaotic systems.
In more detail, the original work consisted of a chaotic combination of two random inputs leading to a first CIs-based system named PRIM CI, (chaotic iteration; see []. In this last version of the chaotic combination of two inputted entropic streams, we solved all the flaws exhibited by the MARK CI version.
In this book, we study the general problem of constructing digital chaotic systems updated by random iterations from low-dimensional to high-dimensional settings, and establish a general framework of composing them. Our digital chaotic systems updated by random iterations are classified into two types: ODDCS(one-dimensional digital chaotic systems, including integer domain chaotic systems, IDCS, and chaotic bitwise dynamical systems, CBDS, in this category) and HDDCS (higher-dimensional digital chaotic systems). We demonstrate that the associated state networks of our systems are strongly connected, and then further prove that they satisfy the Devaney definition of chaos on the domain of finite precision. In addition, Lyapunov exponents for such systems are also given, analog-digital hybrid circuit and FPGA-based implementations are then provided to show the potential applications of digital chaotic systems updated by random iterations in the digital world. The basic advantage and practical benefits of the proposed approach is that the chaos satisfying Devaneys definition can be generated in the real digital devices by means of the chaos generation strategy controlled by random sequences.
As we intend to use chaos of pseudorandom number generation, we need first to define what chaos is, and how to check the randomness of generated sequences. This is the objective of the two following sections, and this introductory chapter ends with the plan of this book.
1.2 Mathematical Definitions of Chaos
For the sake of completeness, let us first recall various key definitions and properties in the field of the mathematical theory of chaos.
In this section, to prevent any conflicts and to avoid unreadable writings, we have considered the following notations, usually used in discrete mathematics:
The n th term of the sequence s is denoted by
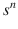
.
The i th component of vector v is
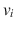
.
The k th composition of function f is denoted by
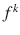
. Thus
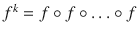
, k times.
The derivative of f is
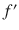
.
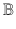
stands for the set
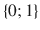
with its usual algebraic structure (Boolean addition, multiplication, and negation), whereas
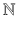
and
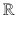
are the usual notations of the respective sets, natural numbers, and real numbers.
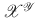
is the set of applications from
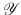
to
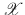
, and thus
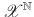
means the set of sequences belonging in
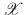
. We use the notation
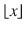
for the integral part of a real x , that is, the greatest integer lower than x . Finally,
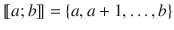
is the set of integers between a and b .
Various explanations of a chaotic behavior for a discrete dynamical system are presented in the following.
1.2.1 Approaches Similar to Devaney












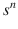 .
.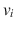 .
.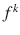 . Thus
. Thus 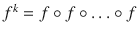 , k times.
, k times.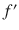 .
.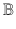 stands for the set
stands for the set 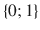 with its usual algebraic structure (Boolean addition, multiplication, and negation), whereas
with its usual algebraic structure (Boolean addition, multiplication, and negation), whereas 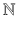 and
and 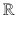 are the usual notations of the respective sets, natural numbers, and real numbers.
are the usual notations of the respective sets, natural numbers, and real numbers. 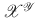 is the set of applications from
is the set of applications from 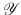 to
to 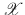 , and thus
, and thus 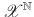 means the set of sequences belonging in
means the set of sequences belonging in 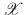 . We use the notation
. We use the notation 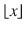 for the integral part of a real x , that is, the greatest integer lower than x . Finally,
for the integral part of a real x , that is, the greatest integer lower than x . Finally, 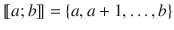 is the set of integers between a and b .
is the set of integers between a and b .