Hans Schwerdtfeger - Hans Schwerdtfeger GEOMETRY OF COMPLEX NUMBERS Circle Geomentry

GEOMETRY OF

COMPLEX

NUMBERS

GEOMETRY OF

COMPLEX

NUMBERS

Circle Geomentry,
Moebius Transformation,
Non-Euclidean Geometry

HANS
SCHWERDTFEGER

Professor of mathematics
McGill University, Montreal

DOVER PUBLICATIONS, INC.
NEW YORK

Copyright 1962 by Hans Schwerdtfeger.

Copyright 1979 by Dover Publications, Inc.

All rights reserved under Pan American and International Copyright Conventions.

This Dover edition, first published in 1979, is an unabridged and extensively corrected republication of the work originally published in 1962 by the University of Toronto Press. The author has added a new Preface, four Appendices and a Supplementary Bibliography to the Dover edition.

International Standard Book Number: 0-486-63830-8
Library of Congress Catalog Card Number:79-52529

Manufactured in the United States of America
Dover Publications, Inc.
31 East 2nd Street, Mineola, N.Y. 11501

IN MEMORIAM

GUSTAV HERGLOTZ

PREFACE TO THE DOVER EDITION

AFTER THE first appearance of this work in 1962, a number of interesting books and monographs were published (Artzy [1], Benz [2], Davis [1], Magnus [1], Pedoe [2], Yaglom [1], [2]), for which my book can serve as collateral or preliminary reading. No major changes have been made; minor errors and misprints have been corrected, some of which have been brought to my attention by readers and reviewers. I am indebted to R. Ping of the University of Kentucky, who pointed out to me a mistake in the formulation of example 4(a) on p. 10. Three appendices have been added in which some recently discovered facts that have bearing on parts of the text are discussed. A fourth appendix draws the readers attention to the book by Yaglom.

I am grateful to Dover Publications for adding my work to their collection of reprints.

February, 1979

H.S.

PREFACE TO THE FIRST EDITION

THIS BOOK develops certain sections of a lecture course on the theory of functions of a complex variable which the author has delivered several times during the last twenty years in several universities in Australia and in Canada. Some of its content does not belong to the standard material dealt with in such a course, but was thought to be useful for a deeper understanding of the geometrical theory of analytic functions as well as of the connections between different branches of geometry.

The first two chapters should be understood by a student who possesses a working knowledge of the algebra of the complex numbers and of the elements of analytical geometry and linear algebra, and in addition a willingness to acquire, in the course of reading, the basic ideas of the (non-infinitesimal) theory of groups of transformations, if necessary by occasionally consulting an introductory text of modern algebra.

The third chapter presents the fundamentals of non-euclidean geometry to a student who is primarily interested in algebra and analysis. It is naturally based upon the first two chapters, but requires more specialized interests in the reader.

Each section is followed by a set of examples. Rather than tax the readers ability, they are designed to convey further information that could not conveniently be incorporated into the main text. In order to invite the readers collaboration in these examples, simple proofs are left to him or short indications are supplied which should enable him to complete a piece of work in all its details.

The centre of interest of the book lies in the intersection of geometry, analysis, and algebra, in general on a moderately advanced level, with occasional views on recent investigations. Much emphasis, however, has been given to the careful exposition of details and to the development of an adequate algebraic technique.

The Bibliography is not intended to be complete. There are two kinds of references: (1) Books and papers of which use has been made in the composition of the text. These are listed under the name of the author and a number in square brackets. Main references in this category are the books by Caratheodory [. (2) Books and articles (not quoted in the text) containing material related to the subject matter, which might be of interest to the reader.

A first draft of the manuscript was critically revised by my friend Peter Scherk. He supplied me with an extensive list of suggestions and corrections which led to substantial improvements in my exposition. It is with pleasure that I record here my gratitude to him for all the time and energy he has spent on my work. I am also grateful to Dr. A. Sherk of the University of Toronto who read the final manuscript and to my colleague, Professor D. Sussman, who read the galley proofs; both made valuable mathematical and linguistic suggestions.

Finally I wish to acknowledge the support and encouragement which I received as Fellow of the Summer Research Institute of the Canadian Mathematical Congress at Kingston in 1958, and more generally, as a new member of the Canadian mathematical community. My thanks are due in particular to the editors of the Mathematical Expositions series and to the University of Toronto Press who kindly accepted my book in their series.

H. S.

April, 1960

These numbers refer to the Supplementary Bibliography (p. 197).

] or [6]). Methods and most of the subject matter in both books are different. Both intend to illustrate the geometrical content of the concept of the complex number system.

CONTENTS

GEOMETRY OF

COMPLEX

NUMBERS

INTRODUCTION

NOTE ON TERMINOLOGY AND NOTATIONS

IN MOST branches of mathematics, including the subject to be dealt with here, a general agreement concerning terminology and notation has not been reached and indeed may not be desirable. The author has tried, however, to introduce such names and terms as have been adopted in the majority of writings on the geometry of complex numbers; he has avoided terms suggesting a special interpretation which he did not wish to emphasize. Thus we speak consistently of circles, avoiding the term chain.

The present exposition starts on the basis of analytical geometry using cartesian coordinates x, y of the points in the plane. These coordinates are any real numbers. For our purposes it is expedient to represent the point (x, y) by the complex number z = x + iy where i = (1). We call x = Re z the real part, y = Im z the imaginary part of z ; also 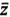= xiy is the conjugate, and |z| = (x2+y2) = r 0 is the modulus or absolute value of z. We notice that z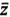 = r2 is zero if and only if z = 0. The elementary algebra of the complex numbers is assumed to be known.

Using polar coordinates r, we may represent the complex number z in the trigonometrical form

z = r(cos +isin ).

We shall call cos + i sin the angular factor of z. It is a complex number of modulus one, commonly denoted by ei. This exponential notation is justified by the identity

ei1 ei2 = ei(1+2),

that is, the functional equation of the exponential function, which is a formal consequence of the addition theorems of elementary trigonometry. Knowledge of the theory of functions of a complex variable will not be assumed ; however, we shall not explain the concepts of continuity and differentiation, which will be used occasionally.

Instead of the angular factor