Livio - The golden ratio the story of phi, the worlds most astonishing number

The Golden Ratio is a book about one numbera very special number. You will encounter this number, 1.61803, in lectures on art history, and it appears in lists of favorite numbers compiled by mathematicians. Equally striking is the fact that this number has been the subject of numerous experiments in psychology.

I became interested in the number known as the Golden Ratio fifteen years ago, as I was preparing a lecture on aesthetics in physics (yes, this is not an oxymoron), and I haven't been able to get it out of my head since then.

Many more colleagues, friends, and students than I would be able to mention, from a multitude of disciplines, have contributed directly and indirectly to this book. Here I would like to extend special thanks to Ives-Alain Bois, Mitch Feigenbaum, Hillel Gauchman, Ted Hill, Ron Lifschitz, Roger Penrose, Johanna Postma, Paul Steinhardt, Pat Thiel, Anne van der Helm, Divakar Viswanath, and Stephen Wolfram for invaluable information and extremely helpful discussions.

I am grateful to my colleagues Daniela Calzetti, Stefano Casertano, and Massimo Stiavelli for their help with translations from Latin and Italian; to Claus Leitherer and Hermine Landt for help with translations from German; and to Patrick Godon for his help with translations from French. Sarah Stevens-Rayburn, Elizabeth Fraser, and Nancy Hanks provided me with valuable bibliographical and linguistic support. I am particularly grateful to Sharon Toolan for her assistance with the preparation of the manuscript.

My sincere gratitude goes to my agent, Susan Rabiner, for her relentless encouragement before and during the writing of this book.

I am deeply indebted to my editor at Doubleday Broadway, Gerald Howard, for his careful reading of the manuscript and his insightful comments. I am also grateful to Rebecca Holland, Publishing Manager at Doubleday Broadway, for her unflagging assistance during the production of this book.

Finally, it is due only to the continuous inspiration and patient support provided by Sofie Livio that this book got written at all.

Numberless are the world's wonders.

S OPHOCLES (495405 B.C. )

The famous British physicist Lord Kelvin (William Thomson; 18241907), after whom the degrees in the absolute temperature scale are named, once said in a lecture: When you cannot express it in numbers, your knowledge is of a meager and unsatisfactory kind. Kelvin was referring, of course, to the knowledge required for the advancement of science. But numbers and mathematics have the curious propensity of contributing even to the understanding of things that are, or at least appear to be, extremely remote from science. In Edgar Allan Poe's The Mystery of Marie Rogt, the famous detective Auguste Dupin says: We make chance a matter of absolute calculation. We subject the unlooked for and unimagined, to the mathematical formulae of the schools. At an even simpler level, consider the following problem you may have encountered when preparing for a party: You have a chocolate bar composed of twelve pieces; how many snaps will be required to separate all the pieces? The answer is actually much simpler than you might have thought, and it does not require almost any calculation. Every time you make a snap, you have one more piece than you had before. Therefore, if you need to end up with twelve pieces, you will have to snap eleven times. (Check it for yourself.) More generally, irrespective of the number of pieces the chocolate bar is composed of, the number of snaps is always one less than the number of pieces you need.

Even if you are not a chocolate lover yourself, you realize that this example demonstrates a simple mathematical rule that can be applied to many other circumstances. But in addition to mathematical properties, formulae, and rules (many of which we forget anyhow), there also exist a few special numbers that are so ubiquitous that they never cease to amaze us. The most famous of these is the number pi (), which is the ratio of the circumference of any circle to its diameter. The value of pi, 3.14159, has fascinated many generations of mathematicians. Even though it was defined originally in geometry, pi appears very frequently and unexpectedly in the calculation of probabilities. A famous example is known as Buffon's Needle, after the French mathematician George- Louis Leclerc, Comte de Buffon (17071788), who posed and solved this probability problem in 1777. Leclerc asked: Suppose you have a large sheet of paper on the floor, ruled with parallel straight lines spaced by a fixed distance. A needle of length equal precisely to the spacing be tween the lines is thrown completely at random onto the paper. What is the probability that the needle will land in such a way that it will intersect one of the lines (e.g., as in )? Surprisingly, the answer turns out to be the number 2/. There fore, in principle, you could even evaluate by repeating this experiment many times and observing in what fraction of the total number of throws you obtain an intersection. (There exist, however, less tedious ways to find the value of pi.) Pi has by now become such a household word that film director Darren Aronofsky was even inspired to make a 1998 intellec tual thriller with that title.

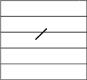
Figure 1

Less known than pi is another number, phi (), which is in many respects even more fascinating. Suppose I ask you, for example: What do the delightful petal arrangement in a red rose, Salvador Dali's famous painting Sacrament of the Last Supper, the magnificent spiral shells of mollusks, and the breeding of rabbits all have in common? Hard to believe, but these very disparate examples do have in common a certain number or geometrical proportion known since antiquity, a number that in the nineteenth century was given the honorifics Golden Number, Golden Ratio, and Golden Section. A book published in Italy at the beginning of the sixteenth century went so far as to call this ratio the Divine Proportion.

In everyday life, we use the word proportion either for the comparative relation between parts of things with respect to size or quantity or when we want to describe a harmonious relationship between different parts. In mathematics, the term proportion is used to describe an equality of the type: nine is to three as six is to two. As we shall see, the Golden Ratio provides us with an intriguing mingling of the two definitions in that, while defined mathematically, it is claimed to have pleasingly harmonious qualities.

The first clear definition of what has later become known as the Golden Ratio was given around 300 B.C. by the founder of geometry as a formalized deductive system, Euclid of Alexandria. We shall return to Euclid and his fantastic accomplishments in Chapter 4, but at the moment let me note only that so great is the admiration that Euclid commands that, in 1923, the poet Edna St. Vincent Millay wrote a poem entitled Euclid Alone Has Looked on Beauty Bare. Actually, even Millay s annotated notebook from her course in Euclidean geometry has been preserved. Euclid defined a proportion derived from a simple division of a line into what he called its extreme and mean ratio. In Euclid's words: