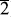Acknowledgments T he authors wish to extend sincere thanks for proofreading and useful suggestions to Dr. Michael Engber, professor emeritus of mathematics at the City College of the City University of New York; Dr. Manfred Kronfeller, professor of mathematics at Vienna University of Technology, Austria; Dr. Bernd Thaller, professor of mathematics at Karl Franzens UniversityGraz, Austria; and Dr. Sigrid Thaller, professor of mathematics at Karl Franzens UniversityGraz, Austria. We are very grateful to Heino Hellwig of the Humboldt UniversityBerlin for contributing the chapter covering biology and for suggestions offered beyond that chapter.
With gratitude we thank Dr. Ana Lucia Braz Dias, professor of mathematics at Central Michigan University, for contributing the chapter on fractals. And to Peter Poole our thanks for some wise suggestions throughout the book. We wish to thank Linda Greenspan Regan for her editorial assistance, Peggy Deemer for her extraordinary expertise in technical editing, and Jade Zora Ballard for putting the book into final shape. Appendix Proofs and Justifications of
Selected Relationships FOR CHAPTER 1: Derivation of the Quadratic Formula The quadratic equation, ax2 + bx + c = 0 (where a > 0), can be solved for x in the following way: ax2 + bx + c = 0. 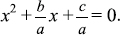
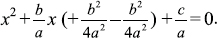
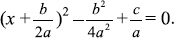 [Add
[Add 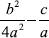 to both sides of the equation.]
to both sides of the equation.] 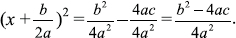 [Take the square root of both sides.]
[Take the square root of both sides.] 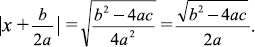 [Note the absolute value.]
[Note the absolute value.] 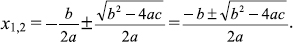 Therefore,
Therefore, 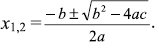 FOR CHAPTER 3: Proof of
FOR CHAPTER 3: Proof of 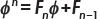 , with n 1 and F0 = 0.
, with n 1 and F0 = 0.
We begin by showing that the statement to be proved by mathematical induction is true for n = 1. Yes, it holds true: 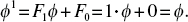 It is also true for the cases of n = 2, 3, 4, 5, as shown below:
It is also true for the cases of n = 2, 3, 4, 5, as shown below: 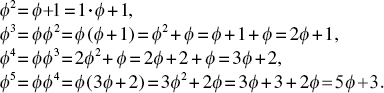 What now remains is that we accept its truth for k:
What now remains is that we accept its truth for k: 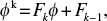 and must show it is then also true for k + 1, namely
and must show it is then also true for k + 1, namely 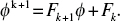 By multiplying the first equation by
By multiplying the first equation by 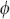 , we get:
, we get: 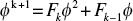 Since
Since 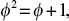 we have
we have 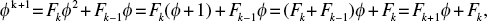 which we were required to show. On Continued Fractions A continued fraction is a fraction in which the denominator contains a mixed number (a whole number and a proper fraction). We can take an improper fraction such as
which we were required to show. On Continued Fractions A continued fraction is a fraction in which the denominator contains a mixed number (a whole number and a proper fraction). We can take an improper fraction such as 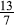 and express it as a mixed number:
and express it as a mixed number: 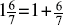 . Without changing the value, we could then write this as
. Without changing the value, we could then write this as 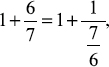 which in turn could be written (again without any value change) as
which in turn could be written (again without any value change) as 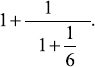 This is a continued fraction. We could have continued this process, but when we reach a unit fraction (as in this case, the unit fraction is
This is a continued fraction. We could have continued this process, but when we reach a unit fraction (as in this case, the unit fraction is 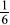 ), we are essentially finished.
), we are essentially finished.
So that you can get a better grasp of this technique, we will create another continued fraction. We will convert 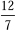 to a continued fraction form. Notice that at each stage, when a proper fraction is reached, take the reciprocal of the reciprocal (e.g., change
to a continued fraction form. Notice that at each stage, when a proper fraction is reached, take the reciprocal of the reciprocal (e.g., change 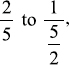 as we will do in the example that follows), which does not change its value:
as we will do in the example that follows), which does not change its value: 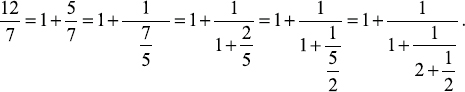 If we break up a continued fraction into its component parts (called convergents), we get closer and closer to the actual value of the original fraction.
If we break up a continued fraction into its component parts (called convergents), we get closer and closer to the actual value of the original fraction.
First convergent of 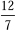 : : | 1. |
Second convergent of 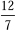 : : | 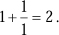 |
Third convergent of 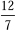 : : | 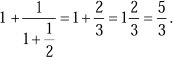 |
Fourth convergent of 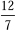 : : | 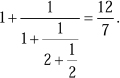 |
The above examples are all
finite continued fractions, which are equivalent to rational numbers (those that can be expressed as simple fractions). It would then follow that an irrational number would result in an
infinite continued fraction. That is exactly the case.
A simple example of an infinite continued fraction is that of 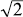 . Although we show it here, we will actually generate it just a bit further on.
. Although we show it here, we will actually generate it just a bit further on. 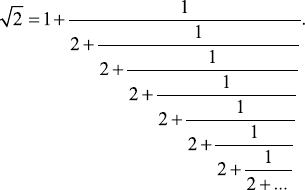 We have a short way to write a long (in this case infinitely long!) continued fraction: [1; 2, 2, 2, 2, 2, 2, 2,], or when there are these endless repetitions, we can even write it in a shorter form as [1;
We have a short way to write a long (in this case infinitely long!) continued fraction: [1; 2, 2, 2, 2, 2, 2, 2,], or when there are these endless repetitions, we can even write it in a shorter form as [1; 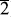
Next page
















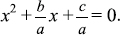
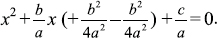
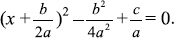 [Add
[Add 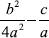 to both sides of the equation.]
to both sides of the equation.] 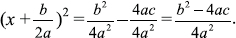 [Take the square root of both sides.]
[Take the square root of both sides.] 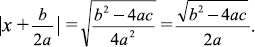 [Note the absolute value.]
[Note the absolute value.] 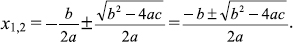 Therefore,
Therefore, 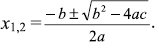 FOR CHAPTER 3: Proof of
FOR CHAPTER 3: Proof of 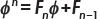 , with n 1 and F0 = 0.
, with n 1 and F0 = 0.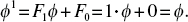 It is also true for the cases of n = 2, 3, 4, 5, as shown below:
It is also true for the cases of n = 2, 3, 4, 5, as shown below: 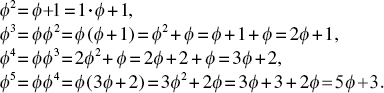 What now remains is that we accept its truth for k:
What now remains is that we accept its truth for k: 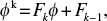 and must show it is then also true for k + 1, namely
and must show it is then also true for k + 1, namely 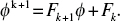 By multiplying the first equation by
By multiplying the first equation by 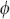 , we get:
, we get: 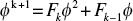 Since
Since 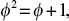 we have
we have 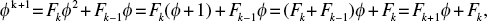 which we were required to show. On Continued Fractions A continued fraction is a fraction in which the denominator contains a mixed number (a whole number and a proper fraction). We can take an improper fraction such as
which we were required to show. On Continued Fractions A continued fraction is a fraction in which the denominator contains a mixed number (a whole number and a proper fraction). We can take an improper fraction such as 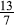 and express it as a mixed number:
and express it as a mixed number: 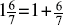 . Without changing the value, we could then write this as
. Without changing the value, we could then write this as 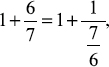 which in turn could be written (again without any value change) as
which in turn could be written (again without any value change) as 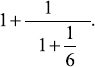 This is a continued fraction. We could have continued this process, but when we reach a unit fraction (as in this case, the unit fraction is
This is a continued fraction. We could have continued this process, but when we reach a unit fraction (as in this case, the unit fraction is 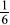 ), we are essentially finished.
), we are essentially finished.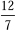 to a continued fraction form. Notice that at each stage, when a proper fraction is reached, take the reciprocal of the reciprocal (e.g., change
to a continued fraction form. Notice that at each stage, when a proper fraction is reached, take the reciprocal of the reciprocal (e.g., change 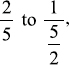 as we will do in the example that follows), which does not change its value:
as we will do in the example that follows), which does not change its value: 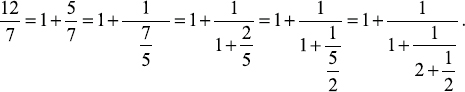 If we break up a continued fraction into its component parts (called convergents), we get closer and closer to the actual value of the original fraction.
If we break up a continued fraction into its component parts (called convergents), we get closer and closer to the actual value of the original fraction.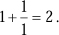
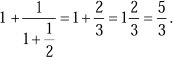
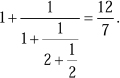
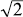 . Although we show it here, we will actually generate it just a bit further on.
. Although we show it here, we will actually generate it just a bit further on.  We have a short way to write a long (in this case infinitely long!) continued fraction: [1; 2, 2, 2, 2, 2, 2, 2,], or when there are these endless repetitions, we can even write it in a shorter form as [1;
We have a short way to write a long (in this case infinitely long!) continued fraction: [1; 2, 2, 2, 2, 2, 2, 2,], or when there are these endless repetitions, we can even write it in a shorter form as [1;